Реализация воспитательной деятельности в общеобразовательной школе ‒ это сложный и непрерывный процесс. Хотя основы воспитания закладываются в дошкольном возрасте, благодаря воздействию семьи, далее к этому присоединяются детский сад и школа, обеспечивают «единство учебной и воспитательной деятельности, реализуемой совместно с семьей и иными институтами воспитания»1. Воспитание детей в школе имеет большое значение для их будущего развития и успешной интеграции в общество, поскольку в этот период жизни происходит формирование личности ребенка, его ценностных и моральных принципов, социальных навыков, которые будут служить основой будущей жизни. Поэтому воспитание стало неотъемлемой частью образовательного процесса.
Воспитательная деятельность в школе, с одной стороны, осуществляется посредством разнообразных школьных мероприятий различных уровней, с другой ‒ непосредственно в ходе учебной предметной деятельности, что отмечается в ФГОС ООО и СОО. В них выделяются три вида образовательных результатов, одним из которых являются личностные результаты, формируемые в процессе различных видов воспитания: гражданское, патриотическое, духовно-нравственное, эстетическое, физическое воспитание, культура здоровья и эмоционального благополучия, трудовое воспитание, экологическое, ценности научного познания. Непрерывность всех видов воспитания обеспечивается за счет их интеграции во все учебные предметы и внеклассные мероприятия, что позволяет реализовывать воспитательную деятельность на протяжении всего образовательного процесса.
Личностные результаты каждого вида воспитания конкретизируются в нормативных документах для любого из учебных предметов на всех ступенях образования. В качестве примера рассмотрим эстетическое воспитание, реализация которого обусловлена не только переломными моментами в современной культуре, но и обязательными требованиями к образовательному процессу, отраженными в ФГОС.
В ФГОС указывается, что эстетическое воспитание включает эстетическое отношение к окружающей действительности; способность воспринимать различные виды искусства и ощущать их эмоциональное воздействие; убежденность в значимости искусства, традиций и народного творчества; готовность к самовыражению в различных видах искусства и стремление проявлять качества творческой личности2.
В ФГОС и Федеральных основных рабочих программах по математике данные личностные результаты в эстетическом воспитании конкретизированы относительно учебного предмета «математика»:
- начальная школа: «уважительное отношение и интерес к художественной культуре, восприимчивость к разным видам искусств, традициям и творчеству своего и других народов; стремление к самовыражению в разных видах художественной деятельности»3;
- 5‒9-е классы: способность к эмоциональному и эстетическому восприятию математических объектов, задач, решений, рассуждений; умение видеть математические закономерности в искусстве4;
- 10‒11-е классы: эстетическое отношение к миру, включая эстетику математических закономерностей, объектов, задач, решений, рассуждений; восприимчивость к математическим аспектам различных видов искусств5.
Однако воспитательная деятельность вызывает немалые затруднения у учителей, что отмечается в статье [1], где авторы указывают также на причины этих затруднений. В рамках выполнения научного проекта «Теоретико-методические особенности развития личностных результатов обучающихся в процессе обучения математике посредством воспитательных возможностей учебного предмета» фонда развития науки ОмГПУ на вебинаре в ноябре 2023 г. нами был проведен онлайн-опрос учителей-предметников общеобразовательных школ города Омска и Омской области. В опросе приняло участие 56 учителей математики: 8 респондентов в возрасте 24‒29 лет, 18 респондентов в возрасте 30‒39 лет, 27 респондентов в возрасте 40‒49 лет, 3 респондента в возрасте 50‒59 лет. Педагогический стаж респондентов распределен в следующих интервалах: 11 человек – до 9 лет стажа, 23 человека ‒ от 10 до 19 лет стажа, 22 человека со стажем более 20 лет. Однако анализ далее представленных результатов не выявил корреляции ни с возрастом, ни со стажем работы.
Цель опроса ‒ определить, вызывает ли затруднение эстетическое воспитание обучающихся в процессе обучения математике, и если да, то каковы причины таких затруднений. Для обработки результатов опроса применен метод процентного соотношения. На вопрос «Возникают ли у Вас трудности в эстетическом воспитании обучающихся средствами математики?» 93 % респондентов ответили «да», 7 % ‒ «иногда».
На вопрос «Каковы причины затруднений при реализации эстетического воспитания средствами математики?» получены следующие ответы:
- отсутствие целенаправленных предметных средств и методических рекомендаций по их включению в процесс обучения (отметили 100 % опрошенных);
- содержание и методический аппарат учебника не позволяют вести эффективную работу по эстетическому воспитанию обучающихся (отметили 93 % опрошенных);
- большая загруженность урока в содержательном плане, чтобы найти место данному материалу (отметили 75 % опрошенных).
На вопрос «Каково место эстетического воспитания в процессе обучения математике?» ответы распределились так: 78 % опрошенных считают, что заниматься данной деятельностью следует на внеурочных занятиях по предмету; 22 % опрошенных думают, что эстетическому воспитанию в равной степени есть место и на уроке, и во внеурочное время.
Анализ результатов опроса показывает, что реализация воспитательной деятельности посредством предмета вызывает большие трудности, и этому есть ряд причин. Большинство опрошенных считают, что заниматься эстетическим воспитанием следует на внеурочных занятиях по предмету. Таким образом, можно сделать вывод о том, что в основном затруднения связаны с методическим обеспечением и временными ресурсами.
Вполне понятно, что большую часть времени у школьника занимают предметные занятия, при этом именно на учителя-предметника, согласно ФГОС, возлагается еще воспитательная работа, в частности по эстетическому воспитанию. Хотя очевидно, что на уроках, например, изобразительного искусства, музыки и литературы такие результаты непосредственно соотносятся с предметными результатами. Таким образом, возникает противоречие: с одной стороны, на уроках математики необходимо реализовывать воспитательные цели, в частности эстетическое воспитание, с другой ‒ на учителя математики возлагается большая ответственность за предметные результаты. Как совместить эти два процесса?
В связи с вышесказанным основной целью нашего исследования является обоснование применения контекстных задач как средства реализации воспитательной деятельности в процессе обучения предмету (на примере эстетического воспитания средствами математики). Для рационального использования времени на уроках математики при сочетании учебной и воспитательной деятельности в процессе изучения содержания учебного материала и решения задач (этому отводится больше половины времени в процессе обучения математике) целесообразно использовать контекстные задачи, объединяющие в себе контекст воспитания и математическую основу.
Существует достаточно много подходов к определению понятия «контекстная задача»:
- «задачи, в которых предметное содержание сплетено с различными сторонами жизни и деятельности человека» [2, с. 78];
- «контекстные задачи обеспечивают прикладную направленность школьного курса математики. Прикладная направленность курса математики напрямую связана с формированием и развитием у учащихся представлений о природе, идеях и методах математики, о характере отражения ею явлений реального мира, о математике как форме описания и методе познания реальной действительности» [3, с. 112];
- задача мотивационного характера, описывающая конкретную жизненную ситуацию, соотносящуюся с социокультурным опытом учащихся, при этом вопрос задачи включает анализ, осмысление и объяснение этой ситуации, в результате разрешения которой обучающийся встречается с учебной проблемой и осознает ее личностно [4];
- задача, адаптируемая к интересам учащегося, она является «способом актуализации его личностного потенциала, пробуждая его к смыслопоисковой деятельности и осознанию им ценности изучаемого материала» [5, с. 100];
- «практико-ориентированная задача, в условии которой описана конкретная жизненная ситуация, отнесенная к субъектному опыту учащегося и осознаваемая им как личностно значимая: требованием которой определяется необходимость: 1) принятия решения на основе имеющихся научных знаний, 2) постановки учебной проблемы» [6, с. 392].
В нашем исследовании под контекстной задачей будем понимать задачу, включающую личностно значимый воспитательный контекст, обеспечивающую прикладную направленность математики и отражающую применение математических методов познания реальной действительности.
Таким образом, контекстная задача, в плане развития личностных результатов обучающихся, содержит описание реальной жизненной ситуации или исторического факта, которые личностно значимы для учащихся и вызывают у них определенные переживания и эмоции.
Выделим особенности контекстных задач, направленных на формирование личностных результатов обучающихся в процессе различных видов воспитания:
- условие задачи может быть сформулировано в виде ситуации, в том числе проблемной, или сюжета, включающего определенный воспитательный контекст (духовно-нравственный, эстетический, патриотический и т. д.) согласно видам воспитания, прописанным в личностных результатах ФГОС;
- получаемый результат должен иметь определенную значимость, обеспечивающую личностное развитие обучающихся. Например, познавательная значимость задачи влияет не только на интеллектуальное развитие обучающихся, но и на различные виды воспитания: через сюжет задачи обучающийся познает вклад математиков в победу в Великой Отечественной войне (патриотическое воспитание); познание математических закономерностей в различных видах искусства (эстетическое воспитание); экологическая значимость формирует бережное отношение обучающихся к окружающей природе (экологическое воспитание);
- в структуре задачи явно или неявно указывается на область применения полученного результата, для получения которого необходимы не только математические знания, но и знания из других предметных областей, в том числе из жизни, на что в задаче нет прямых указаний;
- вопросы к условию задачи направлены на получение результата с помощью средств математики, из которого далее делается личностно значимый вывод.
Выделим принципы составления контекстных задач по математике, направленных на формирование личностных образовательных результатов (в плане воспитания):
- принцип доступности: текст задачи должен быть простым и понятным, без использования абстрактных понятий и соответствовать уровню подготовки;
- принцип релевантности: текст задачи должен соответствовать ее контексту, который значим и актуален для учащихся;
- принцип интеграции: различные виды воспитания должны быть интегрированы не только с содержанием математики, но и с другими аспектами образования и жизни;
- принцип аутентичности: содержание контекстной задачи должно включать достоверную информацию об используемых данных, что важно для предотвращения ее неправильного использования или искажения;
- принцип вариативности: задача должна предполагать различные подходы к ее решению (аналитические, творческие и др.).
Для составления контекстных задач важным этапом является выбор сюжета в соответствии с видом воспитания. В таблице 1 представлены направления выбора сюжетов относительно вида воспитания.
Таблица 1
Направления выбора сюжета для контекстных задач
соответственно видам воспитания
Table 1
Directions for choosing a plot for contextual tasks according
to types of education
| Вид воспитания |
Направление выбора сюжета |
| Гражданско-патриотическое | Электронный фонд правовых и нормативных документов; научные, технологические, спортивные, трудовые и другие достижения народа; памятники своего края и России; государственные символы; история математики (прошлое и настоящее математики как науки через достижения российских математиков); культурное наследие народов России (многонациональность России, величие России и отдельных ее уголков); героические события в истории страны; боевые подвиги народа и др. |
| Духовно-нравственное | Описание жизненных проблемных ситуаций, с которыми сталкиваются люди; личные истории: ситуации, которые вызвали сильные эмоции или заставили задуматься; сюжет книги или фрагмент фильма; СМИ и новости и т. д. |
| Эстетическое | Музыка (музыкальные произведения, инструменты и т. д.); живопись (картины, гравюры и др., биографии художников); архитектура (современные здания, исторические памятники и т. д.); скульптура; литература (сюжеты из литературных произведений); окружающая действительность (животный, растительный мир и т. д.), визуализация математических символов, объектов, рассуждений и т. д. |
| Физическое воспитание, культура здоровья и эмоционального благополучия | Здоровое питание (таблицы содержания белков, жиров, углеводов), советы по рациональному режиму занятий и отдыха, физическая активность (виды спорта, достижения спортсменов, спортивный инвентарь и др.), здоровый образ жизни (вред курения, алкоголя и др.), анатомо-физиологическое развитие человека и др. |
| Трудовое воспитание | Ситуации, предполагающие работу человека в определенной сфере (например, офис банка, магазин, нефтеперерабатывающая промышленность и др.); жизненно-бытовые ситуации (уборка и ремонт дома, покупки, оплата коммунальных услуг и т. д.) |
| Экологическое | Экологические проблемы (изменение климата, загрязнение мирового океана, атмосферы, почвы и грунтовых вод, уничтожение экосистем, истощение природных ресурсов и др.) и их решения (сбор макулатуры, утилизация отходов, высадка деревьев, рациональное использование природных ресурсов) |
| Ценности научного познания | Компоненты математического языка и правила построения предложений с их использованием; история развития математической символики; математические методы познания; сюжеты применения математической науки в различных сферах человеческой деятельности и др. |
Отметим математическую основу контекстных задач относительно видов воспитания: доля, процент, соотношения между величинами, задачи на движение по прямой, совместная работа, стоимость, смеси, сплавы (гражданско-патриотическое воспитание); действия с обыкновенными и десятичными дробями, проценты и отношения, статистические величины и вероятность, последовательность, прогрессии, диаграммы и графики, тригонометрия, многоугольники, круг и др. (физическое и трудовое воспитание); задачи на работу, движение и др., решение уравнений и неравенств (трудовое воспитание); составление таблиц, диаграмм, моделирование процессов, степень с натуральным показателем, решение уравнений, неравенств и др. (экологическое воспитание); обыкновенные и десятичные дроби, функции, геометрические фигуры и их величины, золотое сечение, подобие, координаты, симметрия, преобразования плоскости и пространства и др. (эстетическое воспитание); все направления математического содержания (ценности научного познания).
В каждом виде воспитания выделим направления их реализации средствами математики:
- внутрипредметное (отображает связи определенного вида воспитания между структурными элементами математического содержания). Например, внутрипредметное направление эстетического воспитания включает в себя проявление эстетики в математических объектах, математическом языке и математическом познании;
- межпредметное (отображает связи определенного вида воспитания между структурными элементами математического содержания и структурными элементами других дисциплин и областей знаний). Межпредметное направление эстетического воспитания в математике отображается в различных видах искусства: музыке, живописи, архитектуре, скульптуре, литературе, а также в окружающей нас действительности.
Прежде чем приведем примеры контекстных задач, направленных на развитие личностных результатов в плане эстетического воспитания, отметим, что одним из главных показателей эстетического воспитания является «умение увидеть красоту математики при решении различных задач» [7]. Об умении видеть красоту в математике писал В. Г. Болтянский, отмечая, что красота в математике проявляется в ее изоморфизме между математическим объектом и его наглядной моделью, простоте модели и неожиданности ее проявления [8]. М. С. Мирзоев [7] приводит такие примеры эстетически красивых математических задач, как задача о мостах в Кенигсберге, задача-игра «Кругосветное путешествие по додекаэдру», сводившаяся к обходу всех его вершин по ребрам, их соединяющим, при условии, что ни в одну из вершин нельзя заходить более одного раза.
Рассмотрим примеры составленных нами контекстных задач, направленных на эстетическое воспитание обучающихся средствами математики.
Контекстная задача «Выбор подходящей для ребенка виолончели»
Мензура струнного инструмента ‒ это длина колеблющейся части струны, которая измеряется по струне от верхнего порожка до подставки инструмента (подструнника). Та часть струны, которая находится за подставкой инструмента и при щипке не колеблется, играет немаловажную роль. Эта часть струны при щипке или штрихе смычком компенсирует колебания струны. На рисунке (рис. 1, а) представлены элементы виолончели.
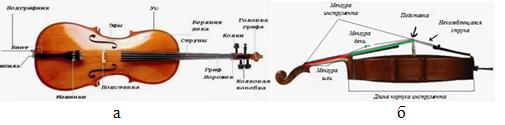
Рис. 1. Элементы виолончели
Fig. 1. Elements of the cello
На виолончели для более комфортного и правильного интонирования мастер регулирует мензуру местоположением подставки. Есть также другие мензуры струнно-смычковых инструментов: мензура шеи ‒ длина от места вылета струны из верхнего порожка до врезки шеи в корпус инструмента; мензура деки ‒ длина от места врезки до местоположения центра ножки подставки. Кроме этих двух мензур, замеряют длину корпуса инструмента. На рисунке (рис. 1, б) представлены эти параметры.
При выборе виолончели для ребенка, прежде всего, необходимо определиться с правильным размером инструмента, который должен соответствовать росту ребенка и длине его вытянутой руки. В противном случае он не сможет комфортно играть. Размеры виолончели: 4/4, 7/8, 3/4, 1/2, 1/4, 1/8. Размер инструмента в дробях не следует рассматривать в качестве абсолютной дроби. Следует понимать, что виолончель размером 1/8 не в восемь раз меньше, чем виолончель размером 4/4. Ее размер составляет около 65 процентов от нормального полного размера 4/4. Виолончель размером 3/4 составляет около 90 процентов от полного размера.
При помощи таблицы можно выбрать подходящий размер виолончели для ребенка. Для удобства в таблице указаны размеры инструмента в миллиметрах и в дробях (табл. 2).
Таблица 2
Таблица подбора виолончели для ребенка
Table 2
Table for selecting a cello for a child
| Длина руки, мм | Рост, м | Возраст, лет | Длина корпуса виолончели, мм | Размер виолончели |
| 420‒445 | 1,1‒1,3 | от 4‒6 | 510‒515 | 1/8 |
| 445‒510 | 1,2‒1,35 | от 6‒8 | 580‒585 | 1/4 |
| 500‒570 | 1,2‒1,45 | от 8‒9 | 650‒655 | 1/2 |
| 560‒600 | 1,35‒1,5 | от 10‒11 | 690‒695 | 3/4 |
| 570‒590 | 1,35‒1,5 | от 10‒11 | 720‒730 | 7/8 |
| От 600 | От 1,5 | от 11 | 750‒760 | 4/4 |
Вопрос: Вася решил научиться играть на виолончели. Но в магазине остался только один вид виолончели со следующими параметрами: мензура шеи 28 см, мензура деки 40 см, а высота подставки 9 см, проекция прямой от вершины подставки до шпиля на плоскость виолончели 8,6 см. Определите размер виолончели. Подойдет ли данный инструмент по размеру мальчику с ростом 162 см и длиной руки 61 см.
При решении данной задачи используются теорема Пифагора и подобие треугольников, поэтому она доступна для решения в 8-м классе. Ее целесообразно предложить на этапе закрепления первого признака подобия (по двум углам). В тексте задачи встречается понятие проекции. С данным понятием учащиеся уже знакомы из учебного предмета «технология», где изучается раздел «Компьютерная графика. Черчение». Однако в случае необходимости в ходе фронтальной работы следует на это обратить внимание. На этапе работы с содержанием контекстной задачи рекомендуется использовать прием смыслового чтения «ИНСЕРТ» (чтение с пометками). В ходе фронтальной работы с учащимися обсуждаются пометки, которые они сделали при чтении задачи: «˅» ‒ знали на данный момент, «-» ‒ думали иначе, «+» ‒ узнали новое, «!» ‒ удивило, «?» ‒ возникли вопросы. Далее возможна работа в парах по поиску решения данной задачи с последующей интерпретацией результатов. В результате учащиеся приходят к выводу о значимости правильных математических расчетов при выборе инструмента, а также при ее конструировании для правильного звучания.
Представленная контекстная задача относится к межпредметному направлению и связывает математику с музыкой, знакомя учащихся с различными музыкальными инструментами. Данная задача знакомит учащихся не только с элементами такого музыкального инструмента, как виолончель, но и показывает значимость математических знаний в ситуации при ее выборе. Контекстные задачи также можно составлять на основе использования ситуаций, уже заложенных в литературных произведениях, что позволяет учащимся освоить математические знания в эстетической форме, а также развить их интерес к чтению художественной литературы.
Например, учащимся можно предложить прочитать отрывок из рассказа Л. Н. Толстого «Много ли человеку земли нужно», суть которого в следующем: Старшина и Пахом заключили между собой сделку: сколько Пахом за день обойдет земли, то вся его будет. Далее описывается передвижение Пахома по земле. На основе данной ситуации учащиеся ставят проблему: «Определить, в каком случае Пахом может получить большую площадь земли?».
Для ответа на этот вопрос учащимся предстоит решить следующие задачи: 1) по данным рассказа установить, какой формы участок обежал Пахом; 2) вычислить площадь этого участка; 3) определить, выгадал Пахом или проиграл от такой формы участка.
В результате исследования задачной ситуации учащиеся приходят к выводам, что Пахом обежал земельный участок в форме прямоугольной трапеции площадью 78 квадратных верст. Однако ему, чтобы достичь намеченного, необходимо было двигаться по окружности длиной 40 верст, и тогда он бы охватил наибольшую площадь участка в 127 квадратных верст.
Данная задача предлагается учащимся 8-го класса при изучении площади трапеции. Площадь круга также доступна учащимся для вычисления, поскольку формула длины окружности и площади круга рассматривается уже в 6-м классе в курсе математики. Задачу можно использовать на этапе создания проблемной ситуации при изучении площади трапеции с последующей организацией исследовательской работы по выводу формулы трапеции различными способами или на этапе закрепления учебного материала в ходе групповой работы. Красота математики проявляется в различных способах решения задачи, выявленной закономерности и неожиданном результате. Данная задача формирует такой показатель эстетического воспитания, как умение видеть математические закономерности в произведениях искусства.
Приведем еще примеры использования литературных произведений для постановки математической задачи:
- отрывок из произведения Жуль Верна «Таинственный остров» можно применять при изучении подобия треугольников;
- басню И. А. Крылова «Лебедь, рак и щука» ‒ при изучении сложения векторов;
- рассказы Н. Н. Носова «Федина задача», Л. Гераскиной «В стране невыученных уроков», Г. Остера «Зарядка для хвоста», А. Аверченко «Экзаменационная задача» ‒ при решении задач арифметическим способом; рассказ А. П. Чехова «Репетитор» ‒ при решении задач алгебраическим и арифметическим способами;
- сказку Л. Кэрролла «Алиса в Стране чудес» ‒ при изучении прямой пропорциональности.
Одним из примеров эстетики математики в природе является умение видеть симметрию в окружающей нас действительности. Здесь учащимся можно предложить контекстную задачу «Симметрия в сервировке стола»:
- на рисунках (рис. 2) представлена сервировка стола. Определить виды симметрии, которые применялись при сервировке. Выявить ошибки в сервировке стола посредством применения симметрии, если они имеются;
- выполнить сервировку стола прямоугольной формы имеющимися предметами, используя разные виды симметрии.

Рис. 2. Сервировка стола
Fig. 2. Table setting
Данную контекстную задачу можно применять уже в 6-м классе после изучения центральной, осевой и зеркальной симметрий на внеурочных занятиях. С 7-го класса полезно рассмотреть в дополнение другие виды симметрии (скользящую и переносную). Применение симметрии в сервировке стола позволяет показать элементы математики в упорядочении объектов, оценить их гармонию. При выполнении данного задания с учащимися можно обсудить влияние принципов симметрии на эстетическое восприятие и достижение визуального равновесия в нем в расположении объектов. Далее можно исследовать вопрос о влиянии геометрии на визуальное восприятие сервировки. Все это способствует формированию эстетического вкуса учащихся посредством применения математических знаний и эстетического отношения к миру в целом.
Применяя контекстные задачи, связанные с проявлением эстетики в архитектуре, можно визуализировать красоту математических объектов в окружающей нас действительности. Приведем фрагмент контекстной задачи «Необычные дома мира». В тексте задачи рассматриваются виды домов, построенных в форме различных математических объектов, в частности пирамиды, и предлагается вычислить коэффициент комфортности такого дома, сделать вывод. Далее рекомендуется исследовать вопрос о существовании домов в форме пирамиды с двумя перпендикулярными основанию гранями, их комфортности и внешней эстетики. В результате исследования учащиеся приходят к неожиданному для них математическому результату о существовании четырехугольной пирамиды с двумя перпендикулярными основанию противоположными гранями. Неожиданный, потому что при ответе на данный вопрос учащиеся дают отрицательный ответ, поскольку ориентируются на то, что все боковые грани пирамиды сходятся в одной точке (вершине пирамиды). Однако неожиданный способ решения данной задачи опровергает их ответ: 1) строим треугольную пирамиду с ребром, перпендикулярным основанию, 2) отсекаем часть пирамиды с перпендикулярным основанию ребром плоскостью, проходящей через вершину пирамиды.
Данная задача относится как к межпредметному направлению эстетического воспитания, так и к внутрипредметному, поскольку показывает внутреннюю красоту математики: в получившемся математическом объекте, способе его получения и математических рассуждениях, что способствует эмоциональному и эстетическому восприятию математических объектов, задач, решений, рассуждений.
Нами также определены содержание математики и соответствующие ему произведения изобразительного искусства, на основе которых составляются контекстные задачи, например: 1. Темы «Симметрия», «Движение», «Подобие»: «Озеро Тан» (Ф. Ходлер), «День и ночь» (М. К. Эшер) и др.; 2. Тема «Окружность и круг. Кольцо»: «Диски» (Р. Делоне); 3. Тема «Взаимное расположение прямых и плоскостей в пространстве»: «Водопад», «Бельведер», «Спускаясь и поднимаясь» (М. К. Эшер); 4. Темы «Выпуклые и невыпуклые многоугольники», «Площадь многоугольника»: «Лом-Лан 2», «Марсан» (В. Вазарели); 5. Темы «Многоугольники», «Метод координат», «Линейная функция» и др.: «Девушки в поле» (К. С. Малевич). Тематика для внеурочных занятий: 1. Тема «Фракталы»: «Предел круга III», «Меньше и меньше» (М. К. Эшер) и др.; 2. Тема «Золотое сечение»: «Мона Лиза» (Л. да Винчи); «Большая волна в Канагаве» (К. Хокусай); 3. Тема «Магические квадраты»: «Меланхолия» (А. Дюрер).
При работе с данным содержанием контекстной задачи у учащихся формируются такие результаты эстетического воспитания, как: способность к эмоциональному и эстетическому восприятию математических объектов и математических закономерностей в искусстве; восприимчивость к математическим аспектам различных видов искусств.
Таким образом, «математические методы исследования помогают раскрыть свойства особенных, важных не только для математики, но и для понимания реального мира эстетически значимых критериев, таких как симметрия, ритм, пропорция, перспектива, гармония, их проявление в музыке, архитектуре, декоративно-прикладном искусстве» [9].
Использование контекстных задач в процессе обучения математике на всех ступенях обучения обеспечивает непрерывное воспитание обучающихся посредством учебного предмета в дополнение к семейному воспитанию и школьному. В процессе такой непрерывной воспитательной деятельности формируется активная жизненная позиция, развиваются кругозор и мировоззрение учащихся, при этом определенную роль играет предметное содержание.
Таким образом, контекстные задачи в воспитании важны, поскольку они связаны с различными аспектами реальной жизни, что позволяет учащимся получить представление о различных ситуациях и проблемах, с которыми они могут столкнуться, а решение задач поможет им научиться анализировать проблемы, определять их причины и находить оптимальное решение. Контекстные задачи в плане эстетического воспитания характерны для математики (как науки, возникшей из практики) в различных видах искусства, они включают хотя и абстрактные объекты, но при этом отражающие реальный мир, проявляющийся в таких эстетических характеристиках, как простота, гармония и неожиданность. Работа с данными задачами позволяет обучающимся смотреть на произведения искусства, объекты окружающей действительности с иной точки зрения, формируя свои эстетические отношения и ценности.
Таким образом, в ходе исследования выделены особенности контекстных задач, направленных на формирование личностных результатов обучающихся в процессе различных видов воспитания; определены принципы составления контекстных задач по математике относительно различных видов воспитания; указаны направления для выбора сюжета задач в контексте различных видов воспитания и направления их реализации средствами математики (межпредметное и внутрипредметное).
Результаты исследования обуславливают его новизну: обоснованы теоретико-методические особенности развития личностных результатов в области эстетического воспитания в процессе обучения наработок посредством решения контекстных задач.
Практическая значимость определяется возможностью использования результатов исследования учителями математики при проведении уроков математики, а также внеурочных занятий, оказывающих воздействие на достижения личностных результатов в области эстетического воспитания.
В первостепенную перспективу внедрения контекстных задач в воспитательную деятельность предмета входят задачи, связанные с разработкой таких задач по каждому виду воспитания и соответствующих методических рекомендаций для учителей.
Список литературы
- Баткаева Я. А., Зачиняева Е. Ф., Туктагулова М. Н. Затруднения учителей в реализации воспитательной деятельности в основной школе: результаты опроса // Непрерывное образование: XXI век. 2021. Вып. 4 (36). DOI: 10.15393/j5.art.2021.7171
- Ахметов М. А. Секреты контекстной задачи // Школьные технологии. 2017. № 1. С. 78–82.
- Далингер В. А. Контекстные задачи как средство реализации прикладной направленности школьного курса математики // Международный журнал прикладных и фундаментальных исследований. 2013. № 10-1. С. 112–113.
- Сериков В. В. Образование и личность. Теория и практика проектирования педагогических систем. Москва : Логос, 1999. 272 с.
- Данильчук В. И., Донскова Е. В., Клеветова Т. В. Контекстные экспериментальные задачи по физике как средство формирования компетенций учащихся // Наука и школа. 2013. № 2. С. 99‒104.
- Шабанова М. В., Форкунова Л. В. Контекстные математические задачи в системе средств формирования финансовой грамотности учащихся // Актуальные проблемы обучения математике и информатике в школе и вузе в свете идей Л. С. Выготского: материалы III Международной научной конференции (17‒19.11.2016 г., МПГУ). Москва : Издательство «Серна», 2016. С. 391‒394.
- Мирзоев М. С. Умение видеть красоту математики при решении задач как показатель математической культуры будущего учителя информатики // Наука и школа. 2010. № 2. С. 51‒55.
- Болтянский В. Г. Математическая культура и эстетика // Математика в школе. 1982. № 2. С. 40‒43.
- Лурье Л. И. Математическое образование в пространстве эстетического опыта // Образование и наука. Известия УРО РАО. 2006. № 6 (42). С. 116‒129.