Стремительное изменение жизни, вызванное цифровизацией, не могло обойти стороной и систему образования. В процессе обучения математике также происходят изменения, связанные с использованием современных возможностей информационных технологий (в том числе онлайн-сервисов), дистанционных образовательных технологий и электронного обучения. Говоря об информационных технологиях в системе обучения в настоящее время, имеем в виду «совокупность технических средств и возможностей глобальной сети, обеспечивающих непрерывное получение и обработку информации с целью ее использования для расширения знаний учащихся» [11, с. 70].
Однако, как показала практика перехода на полное дистанционное обучение в условиях карантина, такой формат неприемлем ни для школьного, ни для вузовского обучения. Процесс обучения требует личного общения педагога и учащихся, которое невозможно полностью заменить изучением видеолекций или выполнением интерактивных заданий (в каком-либо дистанционном курсе или с использованием специальных онлайн-сервисов).
Д. И. Сапрыкина и А. А. Волохович [7] очень подробно и разносторонне представили проблемы и трудности, с которыми столкнулись учителя с переходом на дистанционное обучение, в том числе и в Омской области. Были отмечены проблемы с низким сигналом Интернета, с оснащением техническими средствами для дистанционной работы, кроме этого, увеличилась учебная нагрузка на учителя и учащихся. Проблема отсутствия в школах собственной платформы для обучения учителями решалась посредством использования имеющихся доступных, но нет такой платформы, которая бы охватывала все стороны обучения. Более того, отсутствие методических рекомендаций по использованию цифровых образовательных ресурсов вызывало большие трудности, особенно у учителей с большим педагогическим стажем. «Учителя признаются, что не понимают, как можно проводить занятия без личного контакта с детьми» [7, с. 19].
В связи с этим для успешного использования современных возможностей информационных технологий в процессе обучения целесообразно использовать такие форматы, которые будут обеспечивать и личное общение участников образовательного процесса, и работу с цифровыми ресурсами. Одним из вариантов организации такого процесса в соответствии с поставленными задачами является смешанное обучение.
Существует достаточно много подходов к определению понятия «смешанное обучение», большинство из которых носят описательный характер. Так, смешанное обучение рассматривается как:
- комбинация различных способов доставки образовательного контента, таких как проекты совместной работы, курсы, построенные на веб-технологиях, электронные системы поддержки выполнения работ или проектов и системы управления образовательным контентом [12];
- «использование в той или иной степени электронного и очного обучения» [9, с. 9];
- «система преподавания, сочетающая очное, дистанционное и самообучение, включающая взаимодействие между педагогом, обучающимся и интерактивными источниками информации, отражающая все присущие учебному процессу компоненты (цели, содержание, методы, организационные формы, средства обучения), функционирующие в постоянном взаимодействии друг с другом, образуя единое целое» [5, c. 13].
Среди отечественных исследователей хотелось бы отметить определение Ю. И. Капустина, который рассматривает смешанное обучение как «целенаправленный, организованный, интерактивный процесс взаимодействия обучающих и обучающихся между собой и со средствами обучения, причем процесс обучения, инвариантный к их расположению в пространстве и времени» [2, с. 17]. В этом определении указывается на возможность применения цифровых образовательных ресурсов как в синхронном, так и асинхронном режиме, что значительно расширяет области применения смешанного обучения.
Постоянное развитие информационных технологий, новые возможности онлайн-обучения позволяют еще больше расширить понятие смешанного обучения, и мы в своей работе будем придерживаться определения, данного в статье О. Б. Даутовой, Е. Ю. Игнатьевой и О. Н. Шиловой: «Смешанное обучение (гибридное) (англ. blended learning) – это модель обучения, в которой гармонично сочетаются формы организации обучения как в реальной (очное, лицом к лицу), так и в виртуальной образовательной среде и самообучение» [10, с. 3].
Таким образом, можно выделить три основные составляющие смешанного обучения: «1) традиционное прямое личное взаимодействие участников образовательного процесса; 2) интерактивное взаимодействие, опосредованное компьютерными телекоммуникационными технологиями и электронными информационно-образовательными онлайн-ресурсами; 3) самообразование» [3, с. 167].
В зависимости от доли каждой составляющей и способа организации деятельности можно выделить несколько моделей смешанного обучения. Так, H. Staker, M. Horn [13] выделяют следующие модели, представленные на рисунке 1.
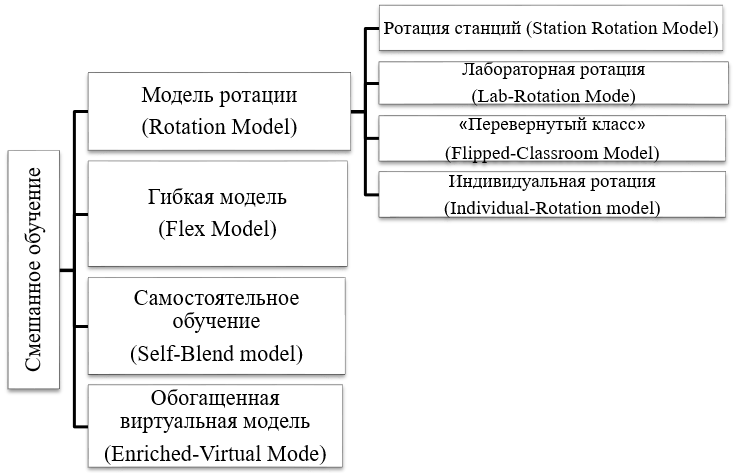
Рис. 1. Классификация моделей смешанного обучения
Fig. 1. Classification of blended learning models
Kлассификация моделей смешанного обучения, немного отличающаяся от предыдущей, также представлена в статье О. Б. Даутовой, Е. Ю. Игнатьевой и О. Н. Шиловой [10]: «Face-to-Face Driver» (лицом к лицу); «Rotation» (поворот, ротация); «Flex» (гибкость); «OnlineLab» (онлайн-лаборатория); «Selfblend» (самостоятельное обучение); «OnlineDriver» (онлайн-встречи). В ней нашли отражение все указанные модели и добавлена модель непосредственного взаимодействия участников образовательного процесса («Face-to-Face Driver»).
Е. Б. Лученкова, М. В. Носков, В. А. Шершнева [4], описывая опыт реализации смешанного обучения в российских школах (НП «Телешкола»), указывают шесть моделей: ротация, автономная группа, перевернутый класс, смена рабочих зон и личный выбор. При этом первые четыре модели предполагают чередование личного общения и работы с цифровыми образовательными ресурсами, а пятая модель предполагает в большей степени самостоятельное изучение дисциплины с использованием электронного обучения и дистанционных образовательных технологий (рис. 2).
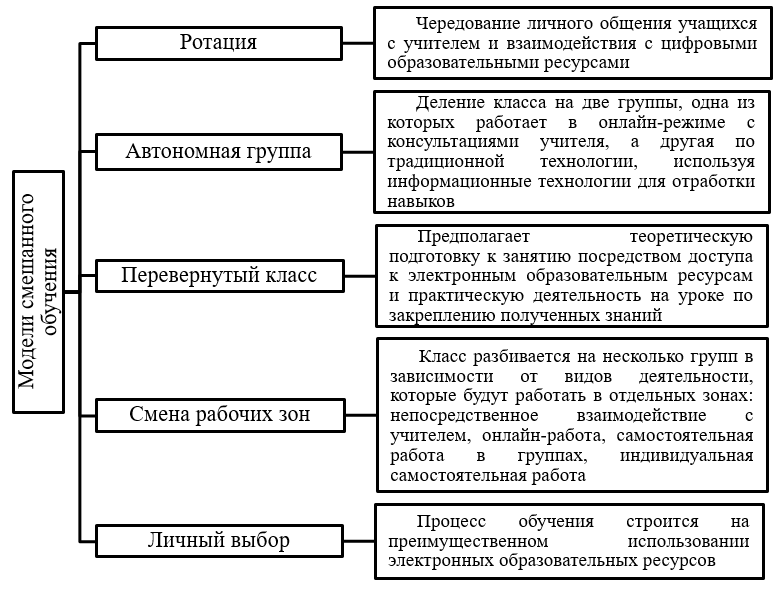
Рис. 2. Особенности организации деятельности учащихся
при реализации разных моделей смешанного обучения
Fig. 2. Features of the organization of student activities in the implementation of different models of blended learning
В своей работе будем использовать указанные модели смешанного обучения (рис. 2), учитывая следующие факторы:
- возраст учащихся (влияет на продолжительность работы с цифровыми ресурсами, сформированность ИКТ-компетенций, готовность к осуществлению самообразования);
- личные качества (развитие математического мышления, математических способностей, сформированность познавательного интереса, навыков учебно-познавательной деятельности);
- специфика изучаемого предмета (абстрактность алгебры, наглядность геометрического материала, практическая значимость полученных математических знаний при изучении смежных дисциплин и в реальной жизни и т. д.);
- возможность представления изучаемого материала с использованием ресурсов цифровой образовательной среды.
Использование моделей смешанного обучения при организации исследовательской деятельности по математике обеспечивает непрерывное математическое образование учащихся, в ходе которого будет формироваться целостная система знаний, в которой каждый элемент учебного материала логически связан с другими и эта связь устанавливается учащимися самостоятельно. Данное направление, безусловно, является актуальным, так как использование возможностей информационных технологий (компьютерные программы, онлайн-сервисы, электронные информационно-образовательные ресурсы и т. д.) дает возможность для организации полноценного исследования, превращая учащихся в «ученых-математиков».
Под исследовательской деятельностью мы понимаем «творческую деятельность, продуктом которой являются новые для учащихся знания, способы действий, методы получения нового знания» [8, с. 14], приобретаемые в результате выполнения исследовательского задания.
В процессе работы над исследовательским заданием учащиеся проходят традиционные «этапы исследовательской деятельности: постановка проблемы, выдвижение гипотезы, проверка гипотезы, оформление результатов исследования, анализ результатов исследования» [8, с. 127].
Смешанное обучение позволяет по-новому подойти к процессу организации исследовательской деятельности учащихся по математике и будет способствовать реализации следующих принципов:
- принцип интерактивности: определяет возможность учащимся получать обратную связь при выполнении исследовательских заданий. Интерактивность должна присутствовать не только при личном взаимодействии учащихся друг с другом и с учителем, но и при их взаимодействии с цифровыми образовательными ресурсами. Учащиеся должны понимать, в верном ли они направлении движутся для достижения поставленных целей исследовательской деятельности. Данный принцип реализуется посредством использования онлайн-форумов, чатов, онлайн-досок, видеоконференции, а также различных активных методов обучения;
- принцип гуманизации: предполагает создание благоприятных, комфортных условий для достижения ситуации успеха при выполнении учащимися исследовательской деятельности и формирования исследовательских умений, с опорой на поддержку в реализации своих потребностей и достижении целей со стороны товарищей и педагогов. Учащиеся всегда могут получить помощь от учителя, в том числе в виде онлайн-консультаций, или от товарищей посредством онлайн-форумов и чатов при самостоятельной работе с образовательными ресурсами;
- принцип индивидуализации: учитывает индивидуальные способности и возможности учащихся, их личностные качества и стремления в процессе организации исследовательской деятельности, а также раскрывает их творческий потенциал. Все это позволяет учитывать темп работы, сложность изучаемого учебного материала, сформированные на начало изучения темы определенные знания, умения и навыки учащихся и тем самым сконструировать индивидуальную исследовательскую карту для выполнения задания в условиях смешанного обучения;
- принцип открытости и гибкости: позволяет вовлечь в исследовательскую деятельность по математике учащихся разных возрастных групп и с разными способностями к такой деятельности, опираясь на индивидуальность каждого обучающегося в освоении математического содержания в условиях смешанного обучения.
Данные принципы дополняют уже известные и широко применимые принципы обучения.
К преимуществам организации исследовательской деятельности учащихся в условиях реализации моделей смешанного обучения можно отнести:
- возможность организации исследовательской математической деятельности с использованием современных цифровых технологий и опорой на имеющиеся знания и опыт учащихся, что позволит обеспечить систематичность математических знаний и непрерывность процесса обучения математике;
- равные возможности при реализации исследовательской деятельности для всех обучающихся независимо от места жительства, состояния здоровья, социального положения и т. д.;
- возможность выстроить индивидуальный образовательный маршрут учащегося с учетом собственного темпа работы, удобного времени и прочих условий;
- доступ к цифровым образовательным ресурсам, что обеспечит учащимся возможность самообразования;
- преобладание самостоятельной познавательной деятельности учащихся с возможностью создания индивидуального (группового) образовательного продукта;
- осуществление подготовки к жизни в условиях цифровизации общества, формирование установки на непрерывное образование (в системе школа ‒ вуз).
Организация исследовательской деятельности учащихся в условиях реализации моделей смешанного обучения математике дает возможности для организации личного общения учащихся с учителем и работы с цифровыми ресурсами различного назначения. В таблице 1 представлены возможные сочетания видов деятельности учащихся на различных этапах проведения исследования для указанных выше моделей смешанного обучения. В таблице используются следующие сокращения: СРОР – самостоятельная работа с образовательными ресурсами, в том числе цифровыми; ЛВУТ – личное взаимодействие с учителем и товарищами в классе.
Таблица 1
Виды деятельности учащихся на разных этапах исследовательской
деятельности, организованной в условиях смешанного обучения
Table 1
Types of student activities at different stages of research activities organized
in a blended learning environment
| Этапы исследовательской деятельности | Модель смешанного обучения | ||||
| Ротация
|
Автономная группа | Перевернутый класс | Смена рабочих зон | Личный выбор | |
| Постановка проблемы | ЛВУТ | ЛВУТ | СРОР | ЛВУТ | ЛВУТ/ СРОР |
| ЛВУТ: анализ проблемной ситуации (анализ математических объектов с выделением существенных и несущественных признаков; синтез как составление целого из частей; сравнение, классификация математических объектов); формулирование проблемы СРОР: выполнение онлайн-упражнений; просмотр учебного видео; анализ проблемной ситуации (анализ математических объектов с выделением существенных и несущественных признаков; синтез как составление целого из частей; сравнение, классификация математических объектов); формулирование проблемы | |||||
| Выдвижение гипотезы | СРОР | ЛВУТ/ СРОР | СРОР | ЛВУТ/ СРОР | СРОР |
| Моделирование; анализ компьютерной модели; экспериментирование; установление причинно-следственных связей, аналогии | |||||
| Проверка гипотезы | ЛВУТ | ЛВУТ/ СРОР | СРОР | СРОР | СРОР |
| ЛВУТ: подведение под понятие, выведение следствий; установление причинно-следственных связей; построение логической цепочки рассуждений, анализ истинности утверждений СРОР: поиск информации в интернет-источниках, учебной литературе; работа с компьютерными моделями; подведение под понятие, выведение следствий; установление причинно-следственных связей; построение логической цепочки рассуждений, анализ истинности утверждений | |||||
| Оформление результатов решения задачи | СРОР | ЛВУТ/ СРОР | СРОР | СРОР | СРОР |
| использование знаково-символических математических средств, построение рассуждений в форме связи простых суждений о математическом объекте, его свойствах; структурирование знаний посредством информационных технологий (ментальные карты, онлайн-доски и др.), подготовка доклада и презентации | |||||
| Анализ результатов исследования (в том числе представление и защита результатов исследования) | ЛВУТ: систематизация полученных результатов и выводов; представление результатов исследования в виде доклада с презентацией; слушание и анализ докладов одноклассников; участие в дискуссии; взаимооценка и рефлексия | ЛВУТ: систематизация полученных результатов и выводов посредством информационных технологий; видеоконференция; представление результатов исследования в виде доклада с презентацией; онлайн-дискуссия: слушание и анализ докладов одноклассников; взаимооценка и рефлексия | |||
При выборе формы (СРОР или ЛВУТ) и вида деятельности учащихся учителю необходимо учитывать принципы индивидуализации, открытости и гибкости.
Отметим, что исследовательская деятельность всегда связана с постановкой проблемы и ее решением, что можно организовать тремя путями:
- создание проблемной ситуации и формулирование проблемы учителем;
- создание проблемной ситуации и формулирование проблемы учителем вместе с учащимися;
- создание проблемной ситуации и формулирование проблемы учащимися.
Третий вариант относится к высокому уровню организации исследовательской деятельности и предпочтителен для модели «перевернутый класс». В зависимости от подготовленности учащихся данный уровень может быть реализован в модели «личный выбор».
Особое значение на данном этапе в формате ЛВУТ приобретает создание проблемной ситуации посредством заданий и вопросов с эмоциями. Например, перед изучением теоремы Пифагора организуется практическая работа (с использованием одной из программ динамической геометрии) по измерению катетов и гипотенузы различных прямоугольных треугольников. Затем учитель, спрашивая значения катетов, угадывает значение гипотенузы, что вызывает у учащихся удивление. Конечно, учитель воспользовался известной формулой, но учащиеся же этого не знают! Так возникает проблема: как связаны между собой два катета и гипотенуза в прямоугольном треугольнике?
В том случае, если проблема формулируется в ходе самостоятельной работы с цифровыми образовательными ресурсами, необходимо подготовить исследовательские карты для фиксации полученных результатов в процессе выдвижения проблемы.
Еще одним важнейшим этапом исследовательской деятельности учащихся является выдвижение гипотез, которое может осуществляться:
- на основе опыта, эксперимента;
- путем рассуждений от частного к общему или наоборот;
- путем проведения аналогии с опытом прошлой деятельности;
- на основе интуиции.
В процессе смешанного обучения математике первый путь целесообразнее реализовать в форме СРОР посредством использования математических конструкторов или подготовленных учителем интерактивных компьютерных моделей, под которыми будем понимать модели, созданные с использованием компьютерных программ, позволяющие получить дополнительную информацию об объекте посредством изменения его параметров [1], что предоставляет возможности для проведения опытно-экспериментальной работы.
Так, при организации исследовательской деятельности в процессе обучения планиметрии в 8-м классе учащимся может быть предложено исследовательское задание: «Установить свойства медианы произвольного треугольника». Независимо от выбранной модели смешанного обучения этап выдвижения гипотезы в данном случае целесообразней организовать путем проведения компьютерного эксперимента с использованием программ динамической геометрии (Живая геометрия, GeoGebra и т. д.), результаты которого будут фиксироваться в исследовательской карте (табл. 2).
Таблица 2
Исследовательская карта по теме «Свойства медианы треугольника»
Table 2
Research map on the topic «Properties of the median of a triangle»
| Свойство 1 | Медиана и площади двух образованных ею треугольников | |||||||||
| Треугольник | Δ _____ | |||||||||
| Укажите медиану | Медиана ___ | Медиана ___ | Медиана ___ | |||||||
| Образованные медианой треугольники | D_____ | D_____ | D_____ | D_____ | D_____ | D_____ | ||||
| Площадь Δ | ||||||||||
| Гипотеза | ||||||||||
| Свойство 2 | Отношение отрезков медианы, полученных точкой пересечения медиан | |||||||||
| Укажите медиану | Медиана ___ | Медиана ___ | Медиана ___ | |||||||
| Длина отрезка (от вершины до точки пересечения медиан) | ____=_____ | ____=_____ | ____=_____ | |||||||
| Длина отрезка (от точки пересечения медиан до пересечения со стороной треугольника) | ____=_____ | ____=_____ | ____=_____ | |||||||
| Отношение отрезков медианы | 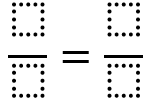 |
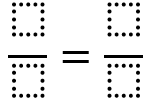 |
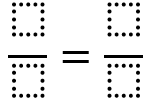 |
|||||||
| Гипотеза | ||||||||||
| Свойство 3 | Площади треугольников, образованных пересечением медиан треугольника | |||||||||
| Треугольники | D____ | D____ | D____ | D____ | D____ | D____ | ||||
| Площади Δ | ||||||||||
| Гипотеза | ||||||||||
В зависимости от выбранной модели смешанного обучения на этапе подготовки к занятию, учитывая принцип индивидуализации, учителем должна быть разработана соответствующая компьютерная модель или подготовлены рекомендации для учащихся по ее созданию в конкретной программе.
Так, если для проведения занятия выбрана модель «Ротация», то в течение одного урока учащиеся должны «пройти» все основные этапы исследовательской деятельности, поэтому в целях экономии учебного времени предлагается готовая модель, выполненная учителем в программе «Живая геометрия» (рис. 3).
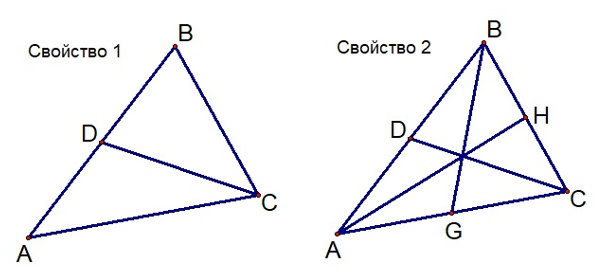
Рис. 3. Компьютерные модели для установления свойств медианы
Fig. 3. Computer models for establishing the properties of the median
Если на уроке планируется использовать модель смешанного обучения «Смена рабочих зон», которая предполагает разделение учащихся по группам, то предложенные выше модели могут быть даны без обозначений, что позволит учащимся выбрать их самостоятельно и в дальнейшем сформулировать гипотезу в самом общем виде.
Если при изучении этой темы планируется использовать модель смешанного обучения «Перевернутый класс», то учащимся следует дать алгоритм самостоятельного выполнения исследовательского задания с помощью компьютерной программы (табл. 3), в которой они создадут модель и проведут исследование согласно предложенной выше карте. На уроке же будет организована работа по доказательству сделанных предположений и решению задач.
Таблица 3
Алгоритм подготовки модели для проведения исследования
по теме «Свойства медианы треугольника»
Table 3
Algorithm for preparing a model for research on the topic «Properties of the median of a triangle»
| Построение | Выполнение в программе «Живая геометрия» |
| Построение треугольника с использованием инструмента «линейка» | 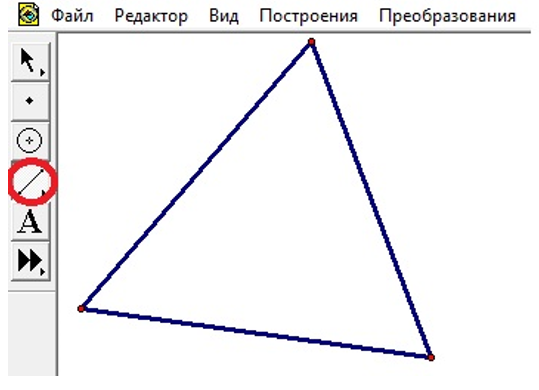 |
| Обозначение вершин треугольника | 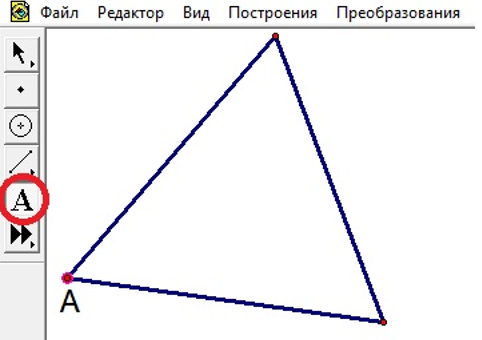 |
| Построение середины отрезка | Выделить нужный отрезок  ‒ выбрать меню «Построения» ‒ команда «Середина» ‒ выбрать меню «Построения» ‒ команда «Середина» |
| Построение медианы треугольника | 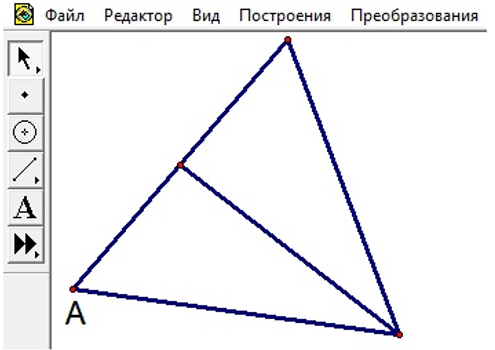 |
| Нахождение площади треугольника | 1) Выделить вершины треугольника ‒ выбрать меню «Построения» ‒ команда «Внутренняя область» 2) Выбрать меню «Измерения» ‒ команда «Площадь» 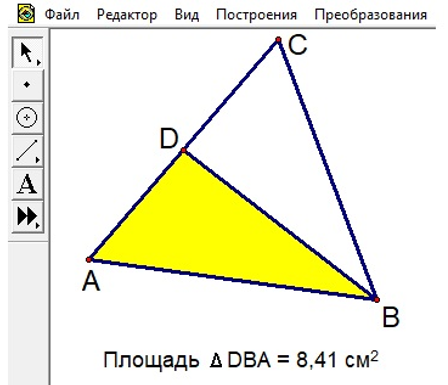 |
Остальные пути выдвижения гипотез могут быть использованы при проведении коллективного мозгового штурма (модель «Смена рабочих зон») или в ходе личного взаимодействия учащихся и учителя (модели «Ротация», «Автономная группа»).
Проверка гипотезы или ее доказательство ориентированы на «поиск учащимися способов решения исследовательской задачи, нахождение альтернативных способов и их взаимосвязей, что обеспечивает “открытие” новых знаний, их углубление и систематизацию» [9, с. 26]. Работу по проверке гипотез в смешанном обучении целесообразнее организовать в форме СРОР, используя те цифровые ресурсы, которые были предложены учащимися на этапе выдвижения гипотезы.
На этапе анализа результатов исследования учащиеся соотносят действия с условием и требованием задачи, проводят обобщение или конкретизацию задачи по необходимости, определяют возможность использования полученных результатов при решении математических задач. Данный этап во всех моделях смешанного обучения организуется в форме ЛВУТ, так как предполагает представление и защиту полученных результатов.
При выборе модели «Личный выбор» исследовательская деятельность учащихся может быть организована посредством дистанционного курса, структура которого соответствует этапам исследования. При этом:
- постановка проблемы и выдвижение гипотезы организуются с помощью готовых интерактивных моделей или посредством самостоятельного составления модели учащимися в математических конструкторах;
- проверка гипотезы учащимися организуется путем изучения теоретического материала, представленного в разных вариантах (видеолекция, интерактивная лекция, текстовый электронный документ и др.).
Результаты исследования учащиеся предоставляют в электронном формате в виде презентации, буклета, интерактивной модели и др.
Например, в программе Advanced Grapher (рис. 4) целесообразно организовать исследование значений параметра а, при каждом из которых система имеет ровно два различных решения:
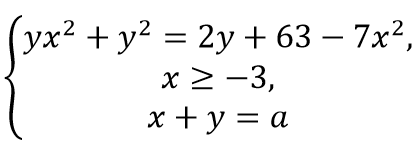

Рис. 4. Построение и исследование графика функции
в программе Advanced Grapher
Fig 4. Рlotting and researching a functional graphin the Advanced Grapher program
По графику функции (рис. 4) в ходе исследования учащийся приходит к выводу, что исходная система имеет ровно два различных решения при
a ϵ [-10; -3] и при а = 9.25.
Непрерывность в организации исследовательской деятельности можно отобразить в виде схемы: «ознакомительно-исследовательская деятельность (дошкольный возраст) → поисково-исследовательская деятельность (начальная школа) → учебно-исследовательская деятельность (основная школа)→ научно-исследовательская деятельность (старшая школа)» [6, с. 130].
Рассматривая организацию исследовательской деятельности в школе на различных ступенях, учитывая принцип открытости и гибкости, выделим соответствующие им модели смешанного обучения (рис. 5).
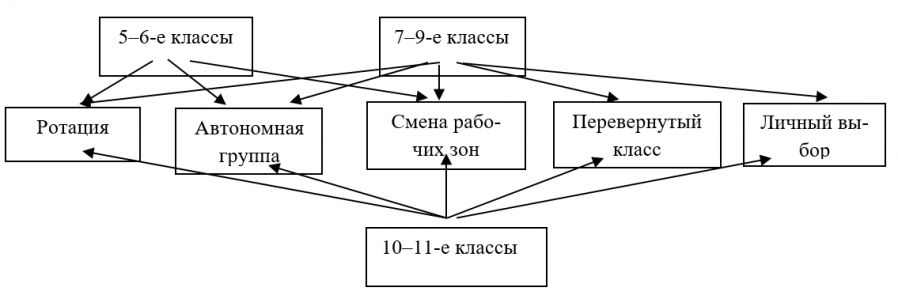
Рис. 5. Выбор модели смешанного обучения для организации исследовательской деятельности по математике
Fig. 5. Choosing a blended learning model
for organizing research activities in mathematics
Организация исследовательской работы в рамках модели «Перевернутый класс» и «Личный выбор» целесообразнее в основной и старшей школе, поскольку данная модель требует самостоятельной деятельности почти на всех этапах выполнения исследовательского задания. Более того, модель «Личный выбор» подходит для учащихся с индивидуальными образовательными потребностями: школьники с высоким уровнем освоения программы и те, кто нуждается в коррекции познавательной сферы. Модели «Ротация», «Автономная группа», «Смена рабочих зон» подходят для всех ступеней образования.
Н. В. Любомирская, Е. Л. Рудик, Т. Е. Хоченкова подчеркивают, что «смешанное обучение обеспечивает вовлеченность в учебный процесс 100 % обучающихся» [3, с. 166]. Организация исследовательской деятельности в указанном формате позволяет каждому учащемуся класса пройти все этапы учебного исследования по математике, поскольку переход на другой этап обеспечивается интерактивным контролем со стороны цифровых ресурсов, взаимоконтролем товарищей и направляющим контролем со стороны учителя.
Таким образом, в процессе организации исследовательской деятельности учащихся по математике в условиях смешанного обучения существенно меняется позиция педагога: учитель выстраивает и направляет деятельность учащихся, а также оказывает им поддержку в выполнении исследовательского задания. Использование моделей смешанного обучения в соответствии с выделенными принципами организации исследовательской деятельности по математике позволяет учесть не только уровень подготовленности школьника, но и способ восприятия учащимися информации, поскольку в процессе обучения используются, например, готовые компьютерные модели (для визуалов), алгоритмы построения компьютерных моделей (для кинестетов), аудио-, видеоинструкции (для аудиалов). Сочетание различных форм познавательной деятельности (индивидуальная работа с цифровыми образовательными ресурсами, групповая работа и общение с учителем) в условиях смешанного обучения на различных этапах проведения исследования, в ходе которых происходит решение поставленных исследовательских задач, направлено на развитие у учащихся исследовательских умений (выдвигать гипотезы, доказывать или опровергать их и т. д.) на разных ступенях обучения математике в школе, что обеспечивает непрерывность организации их исследовательской деятельности.
В первостепенную перспективу внедрения моделей смешанного обучения в процесс обучения математике, в частности при организации исследовательской деятельности школьников, входят задачи, связанные с разработкой методических рекомендаций для учителей и учащихся, решением проблем организации форм работы учащихся с цифровыми образовательными ресурсами.
Список литературы
- Дербуш М. В. Использование интерактивных компьютерных моделей при изучении производной функции // Актуальные проблемы методики обучения информатике и математике в современной школе: материалы Международной научно-практической интернет-конференции, г. Москва, 24 апреля – 12 мая 2020 г. / под ред. Л. Л. Босовой, Д. И. Павлова. Москва, 2020. С. 295–300.
- Капустин Ю. И. Педагогические и организационные условия эффективного сочетания очного обучения и применения технологий дистанционного образования : автореф. дис. … д-ра пед. наук: 13.00.02 / Капустин Юрий Иванович. Москва, 2007. 40 с.
- Любомирская Н. В. Смешанное обучение как механизм формирования навыков проектной и исследовательской деятельности учащихся / Н. В. Любомирская, Е. Л. Рудик, Т. Е. Хоченкова // Исследователь / Researcher. 2019. № 3 (27). С. 165–180.
- Лученкова Е. Б. Смешанное обучение математике: практика опередила теорию / Е. Б. Лученкова, М. В. Носков, В. А. Шершнева // Вестник Красноярского государственного педагогического университете им. В. П. Астафьева. 2015. № 1 (31). С. 54–59.
- Медведева М. С. Формирование готовности будущих учителей к работе в условиях смешанного обучения : автореф. дис. ... канд. пед. наук: 13.00.01 / Медведева Марина Сергеевна. Нижний Новгород, 2015. 31 с.
- Миронов А. В. Деятельностный подход в образовании. Деятельность учебная, игровая, проектная, исследовательская: способы реализации, преемственность на этапах общего образования в условиях ФГТ и ФГОС : пособие для учителя / А. В. Миронов. Набережные Челны, 2013. 139 c.
- Сапрыкина Д. И. Проблемы перехода на дистанционное обучение в Российской Федерации глазами учителей / Д. И. Сапрыкина, А. А. Волохович ; Национальный исследовательский университет «Высшая школа экономики», Институт образования. Москва, 2020. Сер. Факты образования № 4 (29). 32 с.
- Скарбич С. Н. Формирование исследовательских компетенций учащихся в процессе обучения решению планиметрических задач : учебное пособие / С. Н. Скарбич ; науч. ред. д-р пед. наук, профессор В. А. Далингер. Омск, 2010. 194 с.
- «Точка кипения»: смешанное обучение ‒ технология XXI века / авт.-сост.: Л. Н. Нугуманова, Т. В. Яковенко, Е. Г. Скобельцына. Казань, 2019. 72 с.
- Даутова О. Б. Массовый формат смешанного обучения как движение к цифровой трансформации образования [Электронный ресурс] / О. Б. Даутова, Е. Ю. Игнатьева, О. Н. Шилова // Непрерывное образование: XXI век. 2020. Вып. 3 (31). Электрон. дан. DOI: 10.15393/j5.art.2020.6045 (дата обращения: 24.03.2021).
- Дербуш М. В. Инновационные подходы к использованию информационных технологий в процессе обучения математике [Электронный ресурс] / М. В. Дербуш, С. Н. Скарбич // Непрерывное образование: XXI век. 2020. Вып. 2 (30). Электрон. дан. DOI: 10.15393/j5.art.2020.5689 (дата обращения: 24.03.2021).
- Purnima V. Blended Learning Models [Электронный ресурс]. S. l., 2002. Электрон. дан. URL: https://purnima-valiathan.com/wp-content/uploads/2015/09/Blended-Learning-Models-2002-ASTD.pdf (дата обращения: 24.03.2021).
- Staker H., Horn M. Classifying K-12 Blended Learning [Электронный ресурс]. [San Mateo, CA] : Innosight Institute, 2012. 22 p. Электрон. дан. URL: https://eric. ed.gov/?id=ED535180 (дата обращения: 25.08.2021).