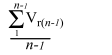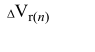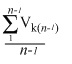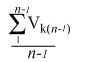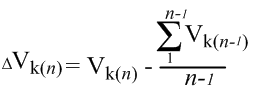Существующая система школьного образования имеет инструменты количественного оценивания качества и уровня обученности детей исключительно по результатам их учебной деятельности. Так построены процедуры измерения всех контрольных и экзаменов. Но анализ только результатов не гарантирует точность и надежность оценки и прогноза успешности дальнейшего образовательного процесса, не позволяет оперативно получать обратную связь ни учителю, ни ученику о характере и качестве совершаемых усилий по освоению образовательной программы. В связи с этим непрерывность образовательного процесса распадается на фрагменты, этапы, ступени, для каждой из которых необходима своя отдельная процедура замера получаемых образовательных эффектов и результатов. Тем самым образовательный процесс только декларируется как непрерывный, но не является таковым по сути.
Вместе с тем наработанные в современной педагогической психологии [4; 6] возможности измерения содержательно-динамических характеристик процессов психического развития человека, в том числе в детском возрасте, дает возможность приступить к разработке методического инструментария, который позволить включать процедуры измерения эффективности учебных и умственных усилий обучающихся непосредственно в процесс непрерывной образовательной деятельности.
Именно этому посвящена данная статья. В качестве материала, на котором будет продемонстрирована возможность разработки и применения подобных процедур, будет использован курс преподавания химии из программы школьного образования. Перед тем, как приступить к непосредственному описанию процедур непрерывной оценки и мониторинга развития способностей учеников на занятиях по химии, очертим круг тех вопросов, в концептуальном контексте которых разрабатывались эти процедуры.
- Как определить способности каждого ученика к обучению химии (или любому другому школьному предмету)?
- Как определить, происходит ли развитие каждого ученика в обучении или нет?
- Как определить «зону ближайшего развития» ученика, чтобы предложить ему наиболее целесообразное задание?
- Как определить оптимальное соотношение заданий репродуктивного и творческого характера?
Без возможности количественно оценить способности ученика и его креативные и репродуктивные компетенции ответить на эти вопросы практически невозможно, хотя рассуждать и теоретизировать об этом можно сколько угодно.
Мы предлагаем концептуально-математическую модель творческих и воспроизводящих (репродуктивных) мыслительных действий при выполнении обучающимся различных учебных заданий, основным предметным содержанием которых является область химии. Рассмотрим способности к обучению химии, которые проявляются прежде всего в самостоятельных действиях учащегося. Мы не будем обсуждать, как ученик понял объясняемый ранее материал и как у него под руководством учителя формировались те или иные умения. Нас интересует этап, когда учащиеся уже выполняют задания самостоятельно и реализуют свои способности независимо от влияния учителя.
В соответствии с предлагаемой нами концептуально-математической моделью уровень развития способностей определяется тем, как ученик справляется с осуществлением воспроизводящих логических действий при выполнении типовых заданий, а также креативных действий при решении творческих задач за определенное время. Наращивание способности решать те или иные задачи мы связываем с изменением показателей скорости и объема осуществляемых учеником мыслительных операций.
Для оценки выполнения задания репродуктивного характера рассмотрим формулу:
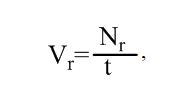
где Vr – скорость воспроизводящих (репродуктивных) логических мыслительных действий; Nr – число воспроизводящих (репродуктивных) действий, выполненных учащимся; t – время, за которое эти действия совершены. Назовем единицу получившейся величины логoчасом (л/ч).
Способность ученика к воспроизводству освоенных знаний и умений решать типовые задачи можно оценивать как среднюю величину скорости его репродуктивной работы на ряде занятий (n):
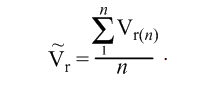
Результат развития способности учащегося к репродуктивному мышлению на конкретном уроке ∆V(n+1) целесообразно рассматривать как разность между скоростью, которую ученик продемонстрировал на данном уроке, и средней скоростью его репродуктивного мышления, сформированной при решении типовых задач на предыдущих уроках:
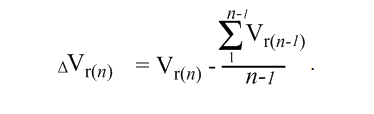
Очевидно, от мотивации ученика, его интеллекта и темпа его мышления зависит время, затраченное на воспроизведение логических действий в процессе самостоятельного выполнения задания. Соответственно величина, характеризующая развитие способности к репродуктивной деятельности ∆Vr(n), у каждого ученика будет индивидуальна, а ее изменение может иметь как положительную, так и отрицательную динамику. Следовательно, эти величины могут быть предметом оценивания эффективности обучения каждого учащегося, выявления динамики его обучения с течением времени, что позволит прогнозировать возможные успехи данного субъекта в обучении воспроизводящего характера в дальнейшем.
Рассмотрим, например, способности учащегося к обучению химии. Возьмем для моделирования процесс изучения учеником 8-го класса темы «Вещества и их превращения». На первом уроке по теме «Становление в науке представлений о простых веществах — металлах и неметаллах» для закрепления знаний и умений в течение 15 мин учащийся выполнил репродуктивные задания к соответствующему параграфу учебника [2]. В таблице 1 представлены репродуктивные логические действия, совершенные им при выполнении каждого задания.
Таблица 1
Репродуктивные действия, совершенные при выполнении заданий
| Номер и формулировка задания | Репродуктивные логические действия | Количество действий |
| 1.Прочитайте описания свойств веществ, на основании которых определите их принадлежность к металлам или неметаллам.
1) Вещество используется человеком в качестве дезинфицирующего средства. В аптеках мы приобретаем 3,5%-ный раствор данного вещества, называемый настойкой. Для приготовления такой настойки темно-серые, блестящие кристаллы растворяют в спирте. Кристаллы данного вещества очень хрупкие. При поднесении к кристаллу электродов лампочка, включенная в цепь, не загорается. 2) Это самое твердое вещество на Земле природного происхождения. Представляет собой прозрачные кристаллы, которые после огранки используются в ювелирном деле. Не проводит электрический ток, плохо проводит теплоту. 3) Вещество не является проводником электричества и плохо проводит теплоту. Своим названием вещество обязано одному из свойств — способности светиться в темноте. Это свойство описал Артур Конан Дойл в повести «Собака Баскервиллей». Однако автор не учел, что это белое пластичное вещество легко испаряется, чрезвычайно ядовито и легко самовоспламеняется на воздухе |
Проанализировал свойства вещества в каждом варианте задания и сделал умозаключение о принадлежности к металлам или неметаллам | 1 х 3 = 3 |
| 2. Почему графит не отнесли к металлам, несмотря на его металлический блеск и электропроводность? | Проанализировал свойства вещества и обосновал ответ | 1 |
| А1. К типичным металлам можно отнести вещество, обладающее следующими физическими свойствами:
1) жидкое, бурое, не проводит электрический ток 2) темно-серое, очень хрупкое, проводит электрический ток 3) желтое, хрупкое, не проводит тепло и электрический ток 4) серебристо-серое, пластичное, электропроводное |
Проанализировал представленные варианты ответа и сделал умозаключение | 1 х 4 = 4 |
Таким образом, за 15 мин (0,25 ч) учащийся совершил 8 логических действий репродуктивного характера.
Вычислим скорость самостоятельного совершения им репродуктивных мыслительных действий:
Vr = 8 / 0,25 = 32 л/ч (логочаса).
Среднюю скорость репродуктивного мышления за предыдущий период условно примем за 32 л/ч. Расчеты логических действий, выполненных учеником самостоятельно на всех уроках изучения темы, позволяют составить таблицу 2 и соответствующий ей график (рис. 1).
Таблица 2
Динамика развития репродуктивного мышления ученика
при изучении темы «Вещества и их превращения» [2]
| Номер урока n | Количество мыследействий Nr | Время t, ч | Скорость репродуктивного мышления, л/ч
Vr(n) = Nr / t |
Уровень репродуктивного мышления (УРМ), л/ч
|
Приращение (развитие) УРМ на каждом уроке, л/ч
|
| 1 | 8 | 0,25 | 32,0 | 32,0 | 0,0 |
| 2 | 13 | 0,33 | 39,4 | 32,0 | 7,4 |
| 3 | 11 | 0,25 | 44,0 | 35,7 | 8,3 |
| 4 | 18 | 0,42 | 42,9 | 38,5 | 4,4 |
| 5 | 20 | 0,42 | 47,6 | 39,6 | 8,1 |
| 6 | 12 | 0,25 | 48,0 | 41,2 | 6,8 |
| 7 | 7 | 0,13 | 53,8 | 42,3 | 11,5 |
| 8 | 19 | 0,33 | 57,6 | 44,0 | 13,6 |
| 9 | 25 | 0,42 | 59,5 | 45,7 | 13,9 |
| 10 | 16 | 0,20 | 80,0 | 47,2 | 32,8 |
| 11 | 25 | 0,25 | 100,0 | 50,5 | 49,5 |
| 12 | 43 | 0,42 | 102,4 | 55,0 | 47,4 |
Из рис. 1 можно сделать вывод, что при изучении этой темы происходит развитие способностей ученика совершать логические действия. Линия приращения развития ученика к репродуктивным действиям имеет устойчивую тенденцию к росту. Это говорит о том, что ученику были подобраны целесообразные задания, попадающие в зону ближайшего его развития. В начале изучения следующей темы можно ожидать от ученика скорости репродуктивных логических действия в пределах 60−120 л/ч. Соответственно это и станет зоной его ближайшего развития. Так, если ученик в течение 20 мин будет выполнять репродуктивные задания, то он в состоянии совершить за это время 18−36 логических действий репродуктивного характера.
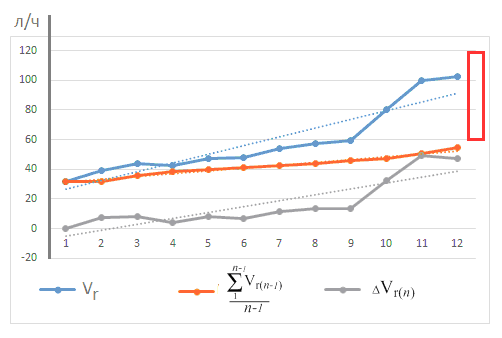
Рис. 1. Поурочная динамика развития способности ученика
совершать репродуктивные логические действия
Используем уже рассмотренную стратегию цифровизации для количественной оценки развития креативного мышления ученика. Для этого возьмем аналогичную формулу:
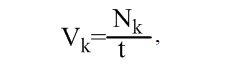
где Vk – скорость креативных мыслительных действий; Nk – количество креативных действий; t – время, затраченное на эти действия.
Единица этой величины была названа нами креачасом (кр/ч).
Принадлежность задачи к творческим определяется ее особыми, в сравнении с типовыми задачами, психодидактическими параметрами [1; 5].
Первый параметр творческой задачи связан с особенностью формулировки ее условия, которая позволяет в процессе решения по-разному его интерпретировать. Это задачи с открытым характером условий, имеющие повышенную степень неопределенности. При решении таких задач, в отличие от обычных школьных репродуктивных заданий, ученик вынужден мыслить дивергентно, а это в большей мере свойственно реальным жизненным ситуациям.
Второй параметр креативных заданий связан с латентностью (скрытостью и неочевидностью) некоторых свойств предметного содержания и, возможно, самой ее проблемы. Соответственно ученик обнаруживает их только в ходе ее решения. Последовательность, упорство и воля при решении задач, обладающих латентными свойствами, характеризует такую особенность мыслительной деятельности ученика, как конвергентность.
Необходимость в процессе решения творческих задач выявлять и переосмысливать интеллектуальные стереотипы является третьим важным их параметром. Такие задачи оказываются проблемно-конфликтными для ученика. Они содержат скрытые противоречия, через столкновение с ними, собственно, и осуществляется преодоление сформировавшихся ранее у учащегося стереотипов. Это позволяет ученику прийти к новым идеям решения.
При количественной оценке решения творческих задач дивергентность мыслительных действий определяется числом рассматриваемых учеником вариантов поиска решения, конвергентность оценивается по глубине проработки каждого варианта решения, оригинальность – по степени радикальности переосмысления имеющихся стереотипов опыта и новизне предложенных решений.
В таблице 3 представлен вариант количественной оценки креативных действий учащегося при решении творческой задачи, осуществленной на основе содержательно-нормативной типологии решений, которая предложена И. Н. Семёновым [1]. Согласно этой типологии, поверхностное решение – это первая пришедшая в голову ученика идея решения задачи как типовой. Тривиальное решение характеризуется воспроизведением таких идей решения, которые уже не лежат на поверхности, но и не отличаются какой-либо оригинальностью. Выгодное решение связано с актуализацией в мыслительном поиске идей уже оригинальных, но скорее уводящих от существа проблемы и подменяющих ее удобным для ученика вариантом ответа (это способ ухода от решения). Близкое решение возникает, когда в процессе работы над задачей появляется действительно перспективная и продуктивная идея, которая еще логически не обоснована и вследствие недостаточной проработанности осталась нереализованной и экспериментально не верифицированной. Проработка же продуктивно оригинальной идеи до логического завершения с понятным обоснованием несостоятельности других возможных вариантов идей позволяет говорить о получении учеником полного творческого решения. Поскольку реальные химические задачи с творческим компонентом требуют не только умозрительного решения, но еще и практической, экспериментальной проверки правильности решения, эта завершающая фаза мыслительно-практических усилий ученика также требует отдельной количественной оценки (табл. 3).
Из данных таблицы 3 следует, что в процессе решения творческой задачи ученик рассматривал четыре идеи решения. Работа над первыми тремя вариантами не позволила ему пойти дальше тривиального решения. Четвертый вариант оказался более перспективным и был доведен до полного творческого решения. В итоге весь объем совершенных в креативном процессе действий можно оценить 28 баллами.
Таблица 3
Пример количественной оценки креативных действий (в баллах)
| Дивергентность
Конвергентность |
Вариант решения | |||
| 1-й | 2-й | 3-й | 4-й | |
| Поверхностное решение | 1 | 1 | 1 | 1 |
| Тривиальное решение | 2 | 2 | 2 | |
| Выгодное решение | 3 | |||
| Близкое решение | 4 | |||
| Полное творческое решение | 5 | |||
| Экспериментальная проверка решения | 6 | |||
Предположим, что учащийся решал творческую задачу 40 мин, и вычислим скорость выполнения творческой работы:
Vk = 28 / 0,6 = 46,7 (кр/ч).
Применяя эту формулу, важно учитывать, что в зависимости от конкретного содержания задачи оценка креативных действий может уточняться. Например, если успешность решения определенной задачи зависит от точности понимания ее условия и глубины проработки его подтекста, то предложенная учеником формулировка продуктивного понимания условия задачи оценивается отдельно 2 баллами. Предложение пооперационного плана экспериментальной проверки той или иной идеи (за исключением проверки варианта полного творческого решения, который оценивается 6 баллами) может быть оценено 3 баллами. Если же в ходе мыслительного поиска состоялось такое переосмысление интеллектуального стереотипа, которое привело ученика к действительно оригинальному решению, то такой креативный результат может быть оценен 10 баллами.
Средняя величина креативной работы, которую ученик выполнил на предшествующих занятиях в соответствии с этими критериями количественной оценки, характеризует его творческие способности (творческую продуктивность). Если ученик работал неровно, то средний результат будет сглаживать экстремальные значения.
Развитие (приращение) творческой способности решать нетиповые задачи, которую учащийся проявил на том или ином занятии (∆Vk), вычисляется как разность между скоростью креативной работы на данном занятии и уровнем (средней скоростью) творческого мышления, проявленного ранее:
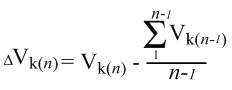
Рассмотрим конкретный пример оценивания процесса креативного мышления ученика при выполнении им различных творческих заданий по химии при изучении темы «Классы неорганических соединений». Предположим, что этот учащийся раз в неделю посещает занятия химического кружка, на которых решает экспериментальные творческие задачи [6]. Кроме того, раз в неделю учитель задает домашнее задание, для выполнения которого требуется поиск дополнительной информации, выходящей за рамки школьного курса химии [3]. В том и в другом случаях ученик совершает креативные действия, которые можно оценить по предложенной методике.
После первого урока учащийся получил задание к §18 [2, с. 102], при выполнении которого нужно было ответить на вопрос: «Из какого металла изготавливали оружие во время восстания Спартака?».
Учащийся за 30 мин совершил действия, указанные в таблице 4.
Таблица 4
Действия при выполнении творческого домашнего задания
| Действие | Количество креативных действий Nk |
| Пытался найти ответ в учебнике | 1 |
| Обратился к поисковику в Интернете | 1 |
| Просмотрел множество сайтов | 1 |
| Выяснил, в какое время было восстание Спартака | 1 |
| Выяснил, какие металлы использовались в это время | 2 |
| Сделал необходимый вывод | 1 |
| Суммарно | 7 |
Определяем скорость креативной работы:
Vk = 7 / 0,5 = 14 (кр/ч).
После второго урока по теме на занятии кружка за 45 мин учащийся, выполнив определенные креативные действия (табл. 5), справился с заданием [3, c. 14].
- «Придумайте, как по своему эскизу изготовить значок или медаль из пластмассы».
Таблица 5
Действия при выполнении творческого задания на занятии кружка
| Действие | Количество креативных действий Nk |
| Сделали эскиз значка (поверхностное решение) | 1 |
| Предложили вырезать значок из пластмассы (тривиальное решение) | 2 |
| Предложили вырезать значок из пенопласта (тривиальное решение) | 2 |
| Предложили сделать форму из пластилина и залить ее эпоксидной смолой | 4 |
| Реализовали идею | 10 |
| Итого: | 19 |
Определяем скорость креативной работы:
Vk = 19 / 0,75 = 25 (кр/ч).
В таблице 6 и на рисунке 2 представлены данные о результатах творческой работы ученика во время изучения рассматриваемой темы.
Таблица 6
Динамика креативных усилий и творческого потенциала ученика
при изучении темы «Вещества и их свойства»
| Номер занятия n | Количество мыследействий Nk | Время t, ч | Скорость креативного мышления, кр/ч
|
Уровень креативного мышления (УКМ), кр/ч
|
Приращение (развитие) УКМ на каждом уроке, кр/ч
|
| 1 | 7 | 0,5 | 14,0 | 14,0 | 0,0 |
| 2 | 19 | 0,75 | 25,0 | 14,0 | 11,0 |
| 3 | 16 | 0,75 | 21,3 | 19,5 | 1,8 |
| 4 | 10 | 0,5 | 20,0 | 20,1 | -0,1 |
| 5 | 9 | 0,5 | 18,0 | 20,1 | - 2,1 |
| 6 | 21 | 0,75 | 21,0 | 19,7 | 1,3 |
| 7 | 10 | 0,5 | 20 | 19,9 | 0,1 |
| 8 | 21 | 1 | 21 | 19,9 | 1,1 |
| 9 | 7 | 0,3 | 23,3 | 20,0 | 3,3 |
| 10 | 23 | 1 | 23 | 20,4 | 2,6 |
| 11 | 11 | 0,5 | 22 | 21,1 | 0,9 |
| 12 | 11 | 0,5 | 22 | 21,1 | 0,9 |
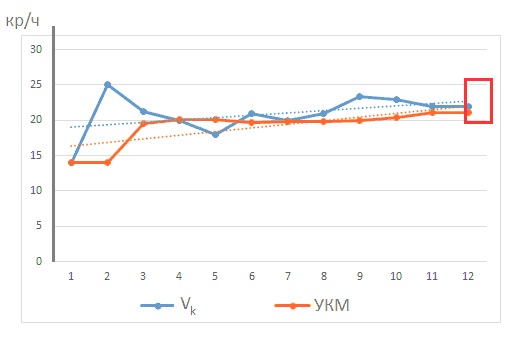
Рис. 2. Динамика развития креативного мышления
при изучении темы «Вещества и их свойства»
Как видно на рисунке 3, от занятия к занятию наблюдается медленный рост развития у ученика скорости креативных действий. Всплеск значения Vk на втором занятии обусловлен особенностью задачи. Вместе с тем можно определить зону ближайшего развития этого ученика – 20−25 кр/ч (отмечена на графике красным).
Рассмотрим динамику приращения креативного развития ученика.
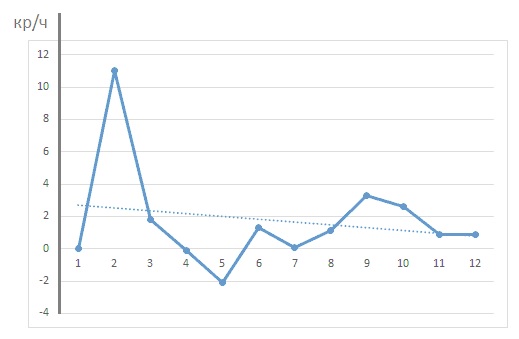
Рис. 3. Динамика приращения креативного развития ученика ( )
Из графика видно, что приращение креативного развития осуществлялось неровно, на некоторых занятиях приращение «уходило» в минусовую область. Из этого можно сделать вывод о том, что ученику предлагались для решения не всегда целесообразные задачи.
Вычисление коэффициента креативности Kk (частного от деления уровней креативных и репродуктивных мыслительных действий соответствующим каждому занятию) позволит проследить тенденцию соотношения развития креативных и репродуктивных действий. Из рисунка 4 следует, что от занятия к занятию имеется тенденция снижения доли креативного развития. В связи с этим возникает вопрос: эта тенденция закономерна или можно найти оптимальное соотношение?
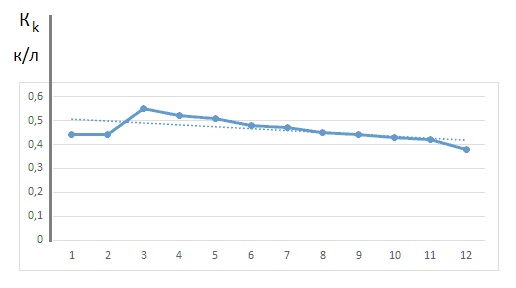
Рис. 4. Динамика изменения коэффициента креативности (Кk)
Подводя итог, скажем, что благодаря предложенным концептуально-математическим моделям можно реально приблизиться к решению практической проблемы цифровизации по крайней мере естественно-научного образования, и в первую очередь его наиболее трудоемкой части. На основании анализа тенденций развития способностей ученика к репродуктивным и креативным действиям можно подбирать наиболее целесообразные задания, соответствующие зоне его ближайшего развития.
Таким образом, данная психолого-педагогическая технология позволит уйти от практики оценки качества и эффективности образовательного процесса только по конечному результату в форме ГИА (ОГЭ и ЕГЭ) и перейти к системе непрерывного мониторинга развития способностей и компетенций обучающихся, т. е. обеспечит переход от скачкообразно-ступенчатого образования к действительно непрерывному.
Список литературы
- Пономарёв, Я. А. Исследование проблем психологии творчества: кол. монография / Я. А. Пономарёв [и др.] ; под ред. Я. А. Пономарёва. – Москва : Наука, 1983.
- Оржековский, П. А. Химия: 8 класс : учебник для общеобразовательных учреждений / П. А. Оржековский, Л. М. Мещерякова, М. М. Шалашова. – Москва : АСТ: Астрель, 2013.
- Оржековский, П. А. Экспериментальные творческие задачи по неорганической химии : книга для учащихся / П. А. Оржековский, В. Н. Давыдов, Н. А. Титов. − Москва : Аркти, 1998.
- Психолого-педагогические и соматические переменные в деятельности современной школе: эффекты кольцевой детерминации / С. Ю. Степанов [и др.] ; под науч. ред. С. Ю. Степанова. – Москва : МГПУ, 2017.
- Психология творчества: общая, дифференциальная и прикладная / Я. А. Пономарёв [и др.]. – Москва : Наука, 1990.
- Степанов, С. Ю. К проблеме выбора стратегии развития цифрового образования как непрерывного / С. Ю. Степанов // Непрерывное образование: XXI век. – 2019. − Вып. 1 (25) [Электронный ресурс]. – Электрон. дан. – URL: DOI: 10.15393/j5.art.2019.4464. − (дата обращения 19.08.2019).