Сегодня как никогда окружающая человека действительность изменяется очень быстро: постоянно появляются новые технические и технологические инновации, социокультурная и экологическая среда непрерывно трансформируется, информационно-коммуникативная сфера развивается с лавинообразной скоростью. Основным драйвером этих изменений, в том числе и в непрерывном образовании [10], становятся цифровые и роботизированные системы с искусственным интеллектом, создаваемые человеком. По мнению мировых экспертов, внедрение автоматизации и цифровизации приведет уже в обозримом будущем к освобождению человека от многих рутинных и репродуктивных действий, требующих от него сегодня больших временных, материальных и физических затрат. По мере становления постиндустриального общества будет расти запрос на неординарный подход к решению самых разных проблем, а значит, потребуются творческие способности человека, применимые во всех сферах его деятельности. Целые кластеры рутинных профессий исчезнут (и это происходит уже сегодня – на наших глазах), на их место придут креативные. В связи с этим назрела необходимость начать в массовой школе готовить подрастающее поколение к творческой деятельности, чтобы, став взрослыми, его представители смогли воспользоваться своими творческими способностями в условиях стремительно развивающегося технотронно-цифрового общества.
Цель развития творческих способностей у современных школьников уже становится одной из приоритетных в российском образовании, что отражено в содержании ФГОСов, где имеются прямые указания на необходимость развивать творческий потенциал обучающихся. И вроде бы эту цель можно было бы считать достигнутой, ведь на международных предметных олимпиадах и в творческих конкурсах наши школьники показывают выдающиеся результаты. Однако, как показывает международные исследования PISA [1], сильной стороной основной массы российских школьников остается способность использования знаний на уровне их воспроизведения по образцам, но они же испытывают большие трудности, когда требуется применить эти знания в незнакомых жизненных ситуациях, предполагающих креативность. На наш взгляд, этому есть несколько возможных объяснений.
1. Развитие творческих способностей обучающихся в современном российском образовании осуществляется избирательно и главным образом во внеурочное время: с так называемыми «одаренными» детьми в предметных кружках или при подготовке их к участию в олимпиадах, но не со всеми ребятами непосредственно в урочное время.
2. Слабая оснащенность предметных курсов и учебников системой творческих задач и заданий, которые необходимы для организации творческой работы непосредственно на уроках. Так, например, проведенный нами анализ основных учебников и учебных пособий, по которым сегодня происходит преподавание курса химии в средней и старшей школе, показал, что практически ни в одном из них таких заданий не содержится. И, конечно, творческие задания можно каждому учителю попробовать составить самостоятельно (правда, без гарантии их качества, т. к. в современных педагогических вузах этому практически не учат) или найти их в специальной методической литературе. Однако большая часть таковой выходит в свет очень малым тиражом или в специальных сборниках, предназначенных главным образом для организации внеурочной деятельности и проведения внеклассных мероприятий, в учебниках же задачи, отвечающие критерию креативности, встречаются крайне редко.
3. Несоответствие формата самих творческих заданий и задач существующим временны́м и поурочно-содержательным регламентам учебного процесса в школе. Как правило, творческие задачи требуют гораздо большего для своего решения времени, чем задачи типового характера. В условиях временного дефицита на уроке и ориентированности содержания учебного процесса на ОГЭ и ЕГЭ чрезвычайно трудно стимулировать творческую деятельность как учащихся, так и учителя.
4. Сложно для педагога осуществить объективное оценивание процесса креативной деятельности обучающихся и ее результатов. Выставление учителем традиционных отметок в условиях непредсказуемости результата творческого поиска может приводить к негативным переживаниям учеников и доминированию у них желания избежать необъективной или низкой отметки, а это работает на сворачивание мотивации их творческого поиска.
Следующие условия, на наш взгляд, позволят организовать творческую деятельность всех обучающихся непосредственно на уроках: 1) разработка или правильный подбор творческих заданий, соответствующих специфике учебного предмета, 2) учет особенностей организации творческого процесса, в отличие от репродуктивной деятельности на уроках, 3) разработанность параметров, критериев и процедур оценки результатов творческой деятельности, 4) использование современных цифровых технологий обработки больших данных (в том числе искусственного интеллекта) для повышения объективации результатов и автоматизации процесса их оценивания в образовательной деятельности.
Рассмотрим психолого-педагогические возможности реализации этих условий на материале преподавания химии в школе.
Следует оговориться, что творческие задания предметного характера достаточно трудно найти даже в пособиях для организации внеурочной деятельности. Поэтому мы опирались на материал сборника «Экспериментальные творческие задачи по неорганической химии» [3].
Кроме того, каждый педагог может попробовать составить их самостоятельно, но все задания должны отвечать, как минимум, следующим требованиям:
- предметное содержание творческой задачи должно соответствовать содержанию программы;
- в условие задачи должны быть включены элементы неопределенности для стимулирования воображения учащихся: последним придется самостоятельно их дорабатывать, домысливая исходные данные и определяя направление своих мыслей;
- отсутствие единственно правильного способа решения – проработка задания должна предполагать возможность нескольких путей решения, из которых учащийся может самостоятельно определить, какой вариант выбрать;
- наличие скрытых или открытых противоречий, которые должны побуждать учащегося к рефлексии (т. е. к преодолению сложившихся у него интеллектуальных и личностных стереотипов), к генерированию и проработке новых для него идей и способов мышления;
- краткость и лаконичность формулировки задания, а также соответствие по уровню сложности выделенному на его решение времени так, чтобы учащийся не почувствовал недостаток времени и смог проявить уже имеющийся у него креативный потенциал.
Выделять на решение подобных задач возможно 10–12 минут (предпочтительно в конце урока, т. к. процесс творческого поиска в начале урока может непредсказуемо трансформировать его ход, что обычно не приветствуется педагогами из-за необходимости строго следовать ритму реализации образовательной программы). Указанные небольшие временны́е затраты позволяют учителю уделить внимание развитию творчества на уроке без ущерба для освоения учебной программы.
Успешность организации творческого процесса во многом зависит от правильно созданной атмосферы. На уроке необходимо создать положительный эмоциональный фон. Перед выдачей задачи учащимся нужно напомнить, что отметка за творческое задание в дневник и журнал не ставится. Особенно настороженно к этому обстоятельству относятся «отличники», которые обязательно задают вопрос об этом, а многие даже после того, как узнают, что отметки не будет, не могут приступить к выполнению задания, поскольку опасаются предложить неверный или, по их мнению, глупый ответ и тем самым «потерять лицо» в глазах учителя.
Не следует сравнивать между собой результаты разных учащихся, динамика творческого развития выявляется только по отношению к предыдущим результатам этого же ученика. Это также очень волнует учащихся, поэтому с самого начала лучше уведомлять ребят о том, что предлагаемая работа направлена на индивидуальный рост их творческих способностей. Торопить и подгонять учащихся при выполнении задания не стоит, поскольку, согласно исследованиям С. Ю. Степанова, И. Н. Семенова и В. К. Зарецкого [5], цейтнот и стресс негативно сказываются на реализации творческого потенциала. Поэтому если учитель стремится к развитию последнего на уроке и готов потратить для этого 10–15 мин., то он должен подобрать подходящее задание и не напоминать детям раз за разом, что до конца его выполнения осталось 5, 3, 2 или 1 минута. Как показали проведенные нами предварительные пробы, десяти минут учащимся вполне достаточно для актуализации своих креативных способностей и именно такое количество времени они активно работают над решением творческого задания, особенно если такие задания предлагать им на уроках регулярно.
Важно поддерживать и подбадривать особенно тех, кто только приступил к выполнению заданий, и тех, кто считает, что то или иное задание ему не по силам. Дело в том, что затруднения на начальном этапе, как правило, возникают из-за неуверенности в себе и сомнений в том, что для решения не хватит имеющихся знаний. Хотя сами творческие задачи построены так, что имеющихся у детей знаний вполне достаточно, и, более того, их избыток может даже мешать выйти на творческое решение, т. к. доступный им опыт скорее выступает как интеллектуальный стереотип, который не позволяет осуществить необычные ходы мысли.
Учитель не регламентирует и не контролирует творческий процесс, не делает прямых подсказок к решению. Но может побуждать учащихся к рефлексии, задавая косвенные вопросы или высказывая общие предположения, и только в том случае, когда они самостоятельно не смогли справиться с возникающими затруднениями. Поэтому важно напомнить учащимся о существовании эвристических и рефлексивных приемов, помогающих приступить к решению задания. При затруднениях, которые испытывают учащиеся на начальном этапе решения задания, учитель предлагает использовать тот или иной эвристический или рефлексивный прием: зарисовать условия задачи в виде схемы, обозначить сильные и слабые стороны способа решения, прочитать задачу в обратном направлении (с конца), сформулировать главные противоречия, предположить что-либо невероятное, не зацикливаться на одном наиболее очевидном решении и т. д.
С целью повышения осмысленности и мотивированности детей в решении нелишне «прорекламировать» задание, обратив внимание на прикладную значимость, раскрыв, чем может быть интересна задача для самих учащихся. Например, для учащихся 9-х классов мы предлагаем задание о захоронении мусора. Известно, что, спустя некоторое время, в местах захоронения отходов токсичные вещества проникают в почву и грунтовые воды. Как это предотвратить? Данное задание действительно актуально сегодня, имеет большой экологический и практический смысл, а значит, может заинтересовать старших школьников своей значимостью в свете охраны окружающей среды. Для учащихся 8-х классов интерес вызывает вопрос о возможностях удаления избытка углекислого газа, образующегося при дыхании на космической станции. Подобный вопрос обычно не задают на уроках химии, но его обсуждение, кроме применения чисто химических знаний, дает возможность проявить смекалку и фантазию.
Предложенная нами методика организации творческой деятельности позволит учителям шире использовать креативные задания предметного характера на уроках, а также повысит интерес учащихся к выполнению как творческих нестандартных заданий, так и к самому предмету химии.
Немаловажным условием организации творческой деятельности на уроке является возможность объективной (т. е. критериально обоснованной) и оперативной оценки результатов деятельности. Для удобства и быстроты процедуры оценивания используются подготовленные заранее протоколы, которые содержатся в специально созданной нами компьютерно-цифровой системе «СREO DATUM»1 (рис. 1).

Рис. 1. Логотип системы «СREO DATUM»
Fig. 1. Logo of the «CREO DATUM» system
Ученики регистрируются в системе с помощью мобильного телефона (планшета, персонального компьютера или иного цифрового гаджета, приспособленного для этих целей) и получают от учителя творческое задание. На экране мобильного телефона появляются две колонки. В первой – учащимся предлагается записывать все найденные варианты решений, а недостатки каждого варианта решения он может вносить во вторую колонку. Компьютерная программа и учитель ориентируют детей так, чтобы они выполняли творческую работу последовательно: сначала предлагали максимальное число вариантов ответа на вопрос задания, а потом приступали к критической оценке каждого варианта, как обычно это делается при процедуре «мозгового штурма».
Программно-компьютерный комплекс системы «СREO DATUM» позволяет собирать и моментально обрабатывать получаемые результаты творческой мыслительной деятельности как отдельного учащегося, так и всего класса в on-line режиме. Это сделано для того, чтобы и учитель, и дети имели возможность получать для себя обратную связь практически сразу же после завершения каждого выполненного ими творческого задания, причем непрерывно на протяжении всех занятий, в которых актуализируется и развивается их творческий потенциал.
Для работы системы «СREO DATUM» были предложены критерии оценки проявления творческой активности учащихся на уроках. Данная разработка опирается на подход, описанной в работе С. Ю. Степанова, П. А. Оржековского, Д. В. Ушакова [4]. На основе этого подхода креативные действия учащегося соответствуют интегральной оценке, которая складывается из таких составляющих, как количество способов решения поставленной задачи и количество выявленных отрицательных сторон каждого решения в процессе их критического переосмысления. Каждый из указанных параметров также имеет свое числовое выражение, которое подсчитывается и визуализируется системой «СREO DATUM» автоматически.
Чтобы понять, как эту задачу решает данная компьютерная программа, рассмотрим в рамках предлагаемой методики более детально процедуру оценивания процесса и результатов творческого мышления. На основе определенного алгоритма программа различает и подсчитывает мыслительные действия дивергентного (D) и конвергентного (К) характера (Дж. Гилфорда [2] и Э. Торранса [7; 9]), осуществляемые учащимися при выполнении предложенного творческого задания. Дивергентные мыслительные действия проявляются в поиске множества вариантов решения одной и той же задачи. Конвергентные же мыслительные действия (К) осуществляются в процессе проработки каждого предложенного направления решения, а также в процессе выстраивания цепочки мыслительных операций, приводящей к наиболее полному и творческому решению задачи.
Таким образом, немного упрощая психологическую сущность двух выделенных сторон творческого мышления с целью большей ее доступности для использования в практической педагогической деятельности, можно сказать, что дивергентность характеризует «широту» творческого поиска, а конвергентность – его «глубину». Очевидно, что оба вида креативных действий – D и К – важны для оценки творческого процесса.
Для количественной оценки дивергентности (D) при выполнении учащимися творческих задач на предметном содержании подсчитывается количество предложенных учеником идей решения, и это является первым критерием количественной оценки креативных действий. При оценке каждого следующего варианта решения, начиная со второго, учитывается повышение трудности выдвижения последующих идей в процессе творческого поиска. Эта трудность возрастает неравномерно и тем больше, чем больше человек исчерпывает очевидные варианты решений, приближаясь к психологическому тупику, а значит, и к необходимости преодолеть довлеющий над ним стереотип мышления, мешающий выйти из этого тупика. В связи с этим мы посчитали уместным использовать для оценки креативности идей числа из ряда Фибоначчи (F), который является общепризнанной числовой последовательностью, отражающей быстрое неравномерное возрастание измеряемого признака в соответствии с «золотой пропорцией». Начиная с третьего члена последовательность выглядит следующим образом: 1, 2, 3, 5, 8, 13 и т. д. [6]. Таким образом, каждый следующий предложенный учеником вариант решения оценивается баллом, который соответствует определенному члену ряда F. Сумма баллов определяет количественную оценку дивергентных мыслительных действий ученика.
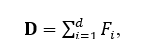
где D – суммарная дивергентность мышления, d – количество ответов, Fi– соответствующий член ряда Фибоначчи.
Если учащийся не предложил ни одного варианта ответа на поставленный вопрос, его дивергентность мышления равна 0.
По аналогии с оцениванием дивергентности конвергентность мыслительных действий вычисляется компьютерной программой как сумма баллов, полученных учащимся за креативные действия, но связанные уже не с количеством и широтой мыслительного поиска, а с глубиной и тщательностью проработки каждого варианта из предложенных направлений решения. Однако поскольку на уроках в силу ограниченности времени обычно нет возможности для осуществления глубокой проработки обучающимися всех идей и способов решения творческой задачи, конвергентные действия предлагается ограничить только критическим анализом предложенных ими же идей решения. Таким образом единицами измерения конвергентных мыслительных действий школьников для предлагаемой методики оценки выступают критические суждения и выявленные недостатки сгенерированных ими же идей и способов решения творческого задания.
Предполагается при этом, что положительные аспекты решения выявляются учащимися уже на этапе выдвижения идей решения, т. е. за счет дивергентных действий. А выявление отрицательных сторон этих идей, препятствий и сложностей в их реализации характеризует конвергентность мышления учащегося.
Таким образом, конвергентность мышления учащегося проявляется в критическом анализе учеником предложенных им идей решения творческой задачи. Если учащийся не нашел ни одного «минуса» к вариантам предложенных им решений, его конвергентность мышления равна 0. Очевидно, что трудность придумывания каждого последующего недостатка в рамках одной идеи тоже является неравномерно растущей и приписываемые баллы за выявленные недостатки предложенных учеником идей также возрастают пропорционально последовательности Фибоначчи (F), а сумма всех баллов есть значение общей конвергентности (К).
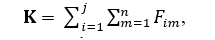
где К – общая конвергентность, j – количество ответов, в которых есть недостатки, n – количество недостатков к i-му варианту ответа, Fim – соответствующий член последовательности F для m-го недостатка к i-му ответу.
В целом количественная оценка креативных действий (КД), которые ученик показал при решении одной задачи, складывается из показателей дивергентности и конвергентности мышления:
КД = D + K.
Такой подход позволяет не только приблизиться к объективной оценке результата творческой деятельности каждого ученика на уроке, но и проследить динамику развития его творческого мышления в рамках школьного курса химии2.
Для наглядности рассмотрим пример количественной оценки креативных действий одного учащегося при выполнении творческого задания. Еще раз подчеркнем, что эта процедура осуществляется системой «СREO DATUM» в автоматизированном режиме.
В нашем примере учащийся предложил 5 идей поиска решения. У первой идеи он нашел 5 недостатков, у второй – 2, у четвертой – 1, для третьей и пятой идей недостатки указаны не были. Отобразим это в таблице 1.
Таблица 1
Пример первичных данных, полученных
при выполнении учащимся творческого задания
Table 1
Example of primary data obtained while students complete a creative task
| Идеи решения | № выявленных недостатков каждой из идей | ||||
| Идея 1 | 1 | 2 | 3 | 4 | 5 |
| Идея 2 | 1 | 2 | |||
| Идея 3 | |||||
| Идея 4 | 1 | ||||
| Идея 5 | |||||
Далее эти данные помещаются в матрицу балльной оценки творческого процесса, построенную с использованием последовательности чисел Фибоначчи (см. табл. 2).
Таблица 2
Матрица балльной оценки творческого процесса
Table 2
Matrix of the creative process score
| Баллы (F) | K | 1 | 2 | 3 | 5 | 8 |
| D | Идеи решения | Выявленные недостатки идеи | ||||
| 1 | Идея 1 | 1 | 2 | 3 | 4 | 5 |
| 2 | Идея 2 | 1 | 2 | |||
| 3 | Идея 3 | |||||
| 5 | Идея 4 | 1 | ||||
| 8 | Идея 5 | |||||
Для расчета количества баллов, которые учащийся получит за каждый вариант ответа и предложенные к нему недостатки решений, в таблице 2 показана последовательность F к дивергентной и конвергентной составляющим (на сером фоне).
Далее эта таблица заполняется значениями из последовательности F в соответствии с положением каждой идеи решения и выявленного недостатка. Суммируя данные в полученной таблице по соответствующему диапазону столбцов, удается количественно оценить дивергентные и конвергентные действия (см. табл. 3).
Таблица 3
Схема подсчета баллов конвергентности, дивергентности и суммарного показателя креативности мышления при решении творческой задачи
Table 3
Scheme for calculating convergence, divergence and total creative thinking scores while solving a creative problem
| 1 | 1 | 2 | 3 | 5 | 8 |
| 2 | 1 | 2 | |||
| 3 | |||||
| 5 | |||||
| 8 | 1 | ||||
| D = 19 | К = 23; ОКД = D + К = 19 + 23 = 42 | ||||
После выполнения учащимися на нескольких уроках творческих заданий оценочные баллы заносятся в сводную таблицу (табл. 4).
Таблица 4
Результаты выполнения учащимися творческих заданий
в течение пяти уроков
Table 4
Students’ results of creative tasks for five lessons
| № задачи | D | K | ОКД |
| 1 | 3 | 8 | 11 |
| 2 | 6 | 5 | 11 |
| 3 | 19 | 11 | 30 |
| 4 | 11 | 18 | 29 |
| 5 | 19 | 23 | 42 |
Построение графиков позволяет получить более наглядное представление о результатах творческой мыслительной деятельности учащегося, тратя всего лишь 10 минут от каждого урока, на которых использовались творческие задания. Эти результаты можно представить тремя графиками для каждого учащегося или для класса целом (см. рис. 2). Для оценки динамики развития творческого потенциала класса удобнее всего использовать средние значения изменения параметров дивергентности, конвергентности и креативности мышления по классу.
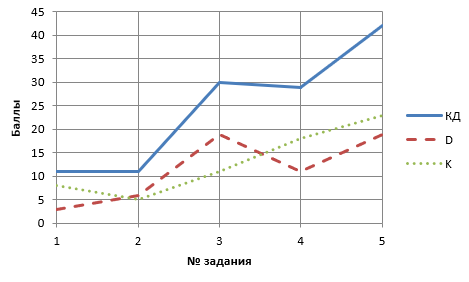
Рис. 2. Графики изменения КД, D, К при выполнении творческих заданий
Fig. 2. Graphs of changes in KD, D, K while performing creative tasks
Первый график (D) показывает траекторию развития дивергентности, второй график (K) – конвергентности мышления, а третий график (KD) – изменения интегрального показателя осуществления креативных действий.
Анализ отдельных показателей для каждого учащегося позволяет системе «СREO DATUM» помочь учителю путем экстраполяции результатов ученика в определении зоны его ближайшего творческого развития. На основании этого учитель в дальнейшем может спланировать как индивидуальную, так и фронтальную работу по развитию творческих способностей учащихся на уроках.
Например, для тех учащихся, у которых наблюдается слабый прирост дивергентности, можно будет подбирать задания, направленные на генерирование большого количества новых идей. Для тех же, у кого недостаточная динамика роста конвергентности, следует предлагать задачи, требующие повышенного внимания ученика к критической проработке каждой его идеи.
Таким образом, несмотря на существенные временны́е ограничения, на уроках возможно организовать систематическую творческую деятельность обучающихся и количественно оценить ее результаты. Непрерывный мониторинг и оценка дивергентных и конвергентных мыслительных действий учащихся при решении ими творческих задач в течение всего предметного курса с помощью системы «СREO DATUM» позволят организовать непрерывный образовательный процесс с учетом творческого развития каждого обучающегося и класса в целом, а также помогут спланировать дальнейшую перспективу их учебной деятельности. В дальнейшем масштабное применение данной методологии и технологии относительно всех предметных курсов как в средней, так и высшей школе поможет повысить эффективность непрерывного образования в условиях его цифровизации с точки зрения творческого развития обучающихся.
Список литературы
- Басюк, В. С. Инновационный проект Министерства просвещения «Мониторинг формирования функциональной грамотности»: основные направления и первые результаты / В. С. Басюк, С. Г. Ковалева // Отечественная и зарубежная педагогика. – 2019. – Т. 1. – № 4 (61) – С. 3–33.
- Гилфорд, Дж. Три стороны интеллекта / Дж. Гилфорд // Психология мышления / под ред. А. М. Матюшкина. – Москва : Прогресс, 1965. – С. 433–457.
- Оржековский, П. А. Экспериментальные творческие задачи по неорганической химии : книга для учащихся / П. А. Оржековский, В. Н. Давыдов, Н. А. Титов. – Москва : Аркти, 1998. – 48 с.
- Степанов, С. Ю. Оценка ученика: на пути к цифровому образованию. Концептуально-математическая модель / С. Ю. Степанов, П. А. Оржековский, Д. В. Ушаков // Народное образование. – 2019. – № 1 (1472). – С. 130–139.
- Степанов, С. Ю. Исследование организации продуктивного мышления / С. Ю. Степанов, И. Н. Семенов, В. К. Зарецкий // Исследование проблем психологии творчества / под ред. Я. А. Пономарева. – Москва : Наука, 1983. – С. 101–133.
- Фибоначчи числа // Энциклопедический словарь юного математика / сост. А. П. Савин – 2-е изд. – Москва : Педагогика, 1989. – С. 312–314.
- Cramond, B. A report on the 40 year follow up of the Torrance Tests of Creative Thinking/ B. Cramond [et al.] // Alive and Well in the New Millennium. Gifted Child Quarterly. – 2005. – № 49. –P. 283–291.
- Livio, M. The Golden Ratio/ M. Livio // The Story of PHI, the World's Most Astonishing Number. – Crown/Archetype, 2008. – 303 с.
- Torrance, E. P. Growing Up Creatively Gifted/ E. P. Torrance // The 22-Year Longitudinal Study. The Creative Child and Adult Quarterly. – 1980. – № 3. – P. 148–158.
- Степанов, С. Ю. К проблеме выбора стратегии развития цифрового образования как непрерывного [Электронный ресурс] / С. Ю. Степанов // Непрерывное образование: XXI век. – 2019. – № 1 (25). – С. 18–27. – Электрон. дан. – DOI: 10.15393/j5.art.2019.4464. − (дата обращения 19.08.2019).