Анализ литературы, наблюдение за учащимися на уроках, беседы со школьниками и учителями показывают, что ученики называют предметы естественно-математического цикла трудными, не всегда понятными. Причин такого положения дел достаточно много. Например, многие учителя считают, что усвоение материала по математике, физике, химии и т. д. зависит от наличия соответствующих способностей. Часто можно услышать мнение: «Ребенок ‒ гуманитарий, поэтому у него и преобладают тройки по естественно-математическим дисциплинам». А так ли это на самом деле?
Одна из причин трудности понимания математики, общей биологии, физики, химии состоит в том, что содержание этих дисциплин достаточно абстрактно. А. К. Сухотин отмечает, что каждая наука не оперирует с непосредственно данными объектами, она абстрагируется от несущественных характеристик, работает с абстрактными результатами, полученными в результате обобщения наблюдаемых явлений [7].
Например, предмет математики ‒ исследование количественных и пространственных отношений, которые присущи всем без исключения объектам реальной действительности. Они характеризуются «своим безразличным отношением к конкретной природе тех предметов, которые они связывают» [4]. Благодаря такому отношению к конкретике возможна широкая применимость математических знаний, методов, теорий в других науках, в практической жизни человека. Эта особенность определяет основную специфическую ее черту – абстрактность.
Специфика естественно-научного знания обуславливает и специфику познания: наличие символического языка, моделирование ситуаций для выявления фактов, их обоснование, специфические для науки методы. Причем каждая наука имеет свой способ моделирования и обоснования истинности высказываемых ею утверждений.
Абстрактность понятийного аппарата дисциплин естественно-математического цикла требует от ученика хорошо развитого словесно-логического мышления. Возникает противоречие. С одной стороны, чтобы усвоить изучаемый материал на уроках математики, физики, химии и др., необходимо владеть логическими операциями (анализ, синтез, обобщение, конкретизация, абстрагирование), с другой ‒ данные логические операции находятся на стадии становления. И этому становлению мышления нужно помочь.
Учителя пытаются решать это противоречие, используя различные технологии: дифференцированное обучение, проблемное обучение, развитие критического мышления, интегрированное обучение и др. Но для успешного применения этих технологий требуется владение учениками логическими операциями: умение анализировать содержание, его обобщать, делать обоснованные выводы и т. д. Значит, решать возникшее противоречие нужно по-другому.
Обратимся к психологии. Во-первых, нужно понимать, что само по себе абстрактное мышление не появится. Психологи отмечают, что мышление возникает из действия. Так, Ж. Пиаже [5] в своих исследованиях показывает, что развитие интеллекта, а вместе с ним и мышления обусловлено развитием операциональных структур интеллекта, в ходе которого мыслительные операции постепенно приобретают качественно новые свойства. Процесс развития интеллекта состоит из трех больших периодов: дооперациональный, конкретных операций, формальных операций. В течение этих периодов происходит зарождение и становление трех основных структур, в которых можно выделить свои стадии. Порядок периодов неизменен. Сначала формируются сенсорно-моторные структуры, т. е. системы обратимых действий, выполняемых материально. Затем возникают и совершенствуются структуры конкретных операций, системы действий, выполняемых в уме, но с опорой на внешние, наглядные объекты. Развитые конкретные операции дают толчок для возникновения формальных операций. Развитие интеллекта переходит на следующую стадию становления формальной логики, школьник овладевает умением формулировать гипотезы, проводить дедуктивные доказательства.
Другой подход к пониманию развития ребенка разрабатывался Л. С. Выготским и его учениками (П. И. Зинченко, А. Н. Леонтьев, Д. Б. Эльконин и др.) в рамках культурно-исторической теории развития человека. Одной из ведущих идей этой теории является понимание развития как соотношения реальной и идеальной форм. Под реальной формой понимаются «наличные и импульсивные способы реагирования» на «свойства предметов», а под идеальной − «та идея, в которой само реагирование становится оформленным, а предметы с их свойствами начинают выступать как опоры плана будущего действия ‒ смысловое поле» [10, c. 27].
Интерпретация данных понятий относительно процесса обучения будет означать следующее. В процессе оперирования предметами ребенок находит основной принцип использования каждого объекта. Этот принцип не просто задан в объекте. Он задан в своей идеальной форме, именно она становится для ребенка особым предметом творческого поиска и преобразования. Идеальное есть форма основного принципа организации определенного знания, определенных способов деятельности, заданных в предметах культуры. Это идеальное может быть присвоено индивидом лишь посредством активной деятельности с предметом. «Идеальная форма материального предмета обнаруживается в способности человека активно воссоздавать его, опираясь на слово, чертеж, модель, в способности превращать слово в дело, а через дело в вещь» [2, c. 35]. Поэтому, по мнению В. В. Давыдова, мышление будет развиваться по схеме: вещь – действие – слово – действие – вещь. В результате реальная форма трансформируется в идеальную, а идеальная в реальную.
А. В. Апраушев, кандидат педагогических наук, много лет проработавший сначала завучем, а потом директором Загорского детского дома для слепоглухонемых детей, подчеркивает: «...язык не существует без предметной основы. Без образов предметов, действий и явлений не может формироваться язык у человеческого существа. Между тем предметы, и прежде всего предметы, включенные в совместную деятельность, и есть та “Золушка”, которая выполняет черновую работу по становлению человеческой психики, предуготавливает формирование высших психических функций» [1, c. 9].
М. А. Холодная обращает внимание на то, что в традиционном обучении приоритет отдается словесно-логическому мышлению и тем самым умаляется значение других видов мышления. Она подчеркивает, что наглядно-действенное и наглядно-образное мышление так же важны для интеллектуального развития, как и словесно-логическое. Они дают другие способы накопления знаний о мире – через действие и через образ. «Однако без подключения и соответствующей организации действенного (и, следовательно, чувственно-сенсорного), а также визуально-пространственного опыта ребенка полноценное усвоение знаков и символов (в том числе и овладение содержанием понятий) затрудняются» [9, с. 176]. М. А. Холодная утверждает, что усвоение знания идет одновременно через чувственное восприятие, использование образов и знаков. «Короче говоря, когда мы нечто понимаем, мы это словесно определяем, мысленно видим и чувствуем» [9, с. 176].
Поэтому схему, предложенную В. В. Давыдовым, имеет смысл уточнить: деятельность по усвоению и воспроизведению знания (превращение реального в идеальное, идеального в реальное) будет идти по схеме: вещь – действие – образ и слово – действие – вещь. Знания, получаемые школьниками по данной схеме, приобретают другое качество. Ученик не просто их усваивает, он их присваивает, они становятся для него живыми.
Здесь нужно заметить, что немецкий психолог К. Фопель предлагает выделить три типа знания по степени его усвоения.
1. Знания, в которых присутствует информация об основных понятиях, законах, концепциях, теоретических сведениях, он называет поверхностными. Знания такого типа присутствуют в книгах, учебниках, справочниках.
2. Знания, в которых отражены способы действия, устанавливаются «внутренние взаимосвязи в рамках определенной дисциплины (с их помощью мы можем понять определенные концепции и теории»), ученый назвал поверхностными [8, с. 9].
3. Третий тип знаний К. Фопель назвал динамическими. Они отличаются от предыдущих двух тем, что позволяют придумывать новые способы действий, становятся ресурсом человека в решениях новых, ранее неизвестных для него задач. Решение задач приносит человеку радость, нет страха перед задачей.
Знания первой и второй групп просто усвоены, часто не имеют эмоциональной окраски, безразличны. Их можно назвать реальной формой знания. При усвоении динамических знаний человек проявляет к ним интерес, появляется желание продолжить поиск, так как он приносит удовольствие, знание получает положительную эмоциональную окраску. Его можно назвать идеальной формой знания.
Для того чтобы знание стало динамическим, нужно задействовать разные способы получения информации: предметное действие, построение образов, моделирование ситуаций, словесное описание и т. д. Практика показывает, что пока еще в большинстве случаев учитель рассказывает ‒ ученик слушает. Вероятно, такое обучение приводит к непониманию учащимися учебного материала.
Понимание взаимосвязи между реальной и идеальной формами знания особо важно для обучения математике, так как при овладении данным учебным предметом учащемуся приходится строить обобщения от уже абстрактных понятий. Остановимся на характерных чертах предмета «математика».
Выше было сказано, естественно-математические науки в большей мере − абстрактные науки. А. К. Сухотин отмечает, что «специфика математики заключается не в том, что она ‒ абстрактная наука, а в природе ее абстракций» [7, c. 28]. Что имеется ввиду? Математический понятийный аппарат – не произвольные понятия, не только абстракции от реально существующих явлений, процессов и предметов, но и абстракции от уже сложившихся абстракций, т. е. абстракции высших порядков. Например, возьмем понятие «число». Сначала оно появляется как результат пересчета предметов (натуральное число), затем как результат выполнения арифметических действий. И если сложение и умножение натуральных чисел всегда возможны, то при выполнении вычитания и деления натуральных чисел возникают проблемы. Появляются отрицательные числа. При делении натуральных чисел не всегда возможно получить результат. Появляются рациональные числа. При работе с площадями часто невозможно извлечь квадратные корни. Появляются действительные числа. Так на базе старых абстракций (натуральное число) строятся новые: целое число, рациональное число, действительное число и т. д. Специфика математических абстракций состоит в том, что они образуют многоступенчатую последовательность разного вида абстракций.
Эта абстрактность математики проявляется в двух ее характерных чертах, которые обуславливают дополнительные трудности у учеников в усвоении математики.
Первая черта заключается в том, что математика не открывает свой объект и его свойства, а его создает, придумывает. А. Реньи следующим образом охарактеризовал этот процесс: «Врач изучает болезни, астроном – небесные тела, естествоиспытатель – живую природу и т. д. Но существовали бы болезни, не будь врачей, звезды без астрономов, природа без естествоиспытателей? Безусловно, существовали бы. Спросим себя, существовали бы числа, не будь математиков? На этот вопрос мы затрудняемся с ответом» [6, c. 23]. Кажется, что математики придумывают свои объекты и инструменты для изучения мира совершенно произвольно. Но это не так. Обобщение и абстрагирование находятся в диалектическом единстве с необходимостью создания именно таких объектов, формулировки таких свойств. Эта свобода создаваемых математикой объектов часто является камнем преткновения для ученика в понимании математики, заставляет его просто зазубривать математические факты.
Вторая характерная черта математики, обусловленная ее абстрактностью, это наличие собственного символического языка, благодаря которому возможно абстрагироваться от внешних свойств объектов окружающего мира и работать с ними, устанавливая только отношения между ними. Действительно, без специальных обозначений при высоком уровне абстракции можно только запутаться во множестве слов и связей между ними.
Подводя итог вышесказанному, приведем слова американского математика, занимающегося вопросами истории и философии математики. М. Клайн пишет: «…математика строит модели целых классов реальных явлений. Понятия, обычно идеализированные (независимо от того, почерпнуты они из наблюдений природы или являются плодами человеческого разума), аксиомы, которые также могут быть подсказаны физическими фактами или придуманы людьми, процессы идеализации, обобщения и абстракции, а также интуиция − все идет в ход при построении моделей. Доказательство цементирует элементы модели воедино» [3, c. 59].
Для разрешения противоречия между абстрактным характером математики и развивающимся логическим мышлением необходимо обеспечить опору для усвоения материала, используя действия с предметами и/или их образами.
Это особая предметность, необходимая для того, чтобы можно было представить, воспроизвести во внешней форме внутренние связи и отношения, закономерности существования познаваемых математических объектов. Наблюдаемые их свойства и связи, опираясь на эту предметность, обобщаются и присваиваются учеником. Познаваемый объект, таким образом, замещается системой абстракций, которую можно назвать моделью. В. В. Давыдов обращает внимание: «Модель – это абстракция особого рода, в которой существенные отношения предметов выражены в наглядно-воспринимаемых и представляемых связях и отношениях знаковых элементов. Это своеобразное единство единичного и общего (т. е. чувственного и абстрактного), при котором на первый план выдвинуто общее, существенное» [2, c. 128]. Использование модели позволяет ученику установить связь между задачей и содержанием его наличного опыта. Эта взаимосвязь помогает ученику опосредованно получить новую информацию об изучаемом объекте, что позволяет выйти за сферу этого опыта, сделать скачок.
Проиллюстрируем сказанное на примере поиска алгоритма сложения обыкновенных дробей. Этот пример не случаен. Если предложить выпускникам школы найти, например, сумму 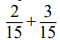 , то всегда получим правильный ответ
, то всегда получим правильный ответ 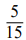 . Но если предложить найти сумму
. Но если предложить найти сумму 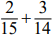 , то практически всегда найдется ученик, и не один, который напишет
, то практически всегда найдется ученик, и не один, который напишет 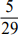 . Такой ответ говорит о том, что ученик не понимает сути получения результата, он не понимает, о чем «рассказывает» дробь. Знания носят поверхностный характер. Чтобы не было таких казусов, полезно идти по схеме, которая обоснована в первой части статьи: вещь – действие – слово и образ – действие – вещь (предметное действие – образ – правило).
. Такой ответ говорит о том, что ученик не понимает сути получения результата, он не понимает, о чем «рассказывает» дробь. Знания носят поверхностный характер. Чтобы не было таких казусов, полезно идти по схеме, которая обоснована в первой части статьи: вещь – действие – слово и образ – действие – вещь (предметное действие – образ – правило).
При знакомстве с дробями полезно использовать набор «Нумикон», палочки Кюизенера, кубики и другие игры. Они обеспечат выполнение предметных действий для понимания абстрактного понятия «дробь», помогут в понимании способов сравнения дробей, выполнения арифметических операций над дробями с одинаковыми знаменателями. Рамки статьи не позволяют подробно описать работу с этим наглядным материалом.
После выполнения действий с предметами ученики рисуют дроби, разбивая на равные части прямоугольники. Например, дробь 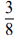 будет можно представить так:
будет можно представить так:

Рисуя дроби, школьники их сравнивают, дроби с одинаковыми знаменателями складывают и вычитают. Перейдем к описанию изучения сложения дробей с разными знаменателями.
Детям предлагаются следующие задачи:

В процессе решения первой задачи ученики отмечают, что для ее решения можно было преобразовать 4 дм в 40 см и найти результат в сантиметрах: 65 см.
В процессе решения второй задачи сначала дети попытались получить ответ в сантиметрах. Но выяснили, что такое решение затруднительно. Тогда они воспользовались прямоугольником и быстро получили ответ.
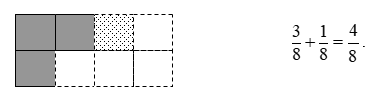
В процессе решения третьей задачи ученики приходят к выводу, что ответить на вопрос задачи они не могут. Ни первый способ нахождения суммы величин (преобразования метра в сантиметры), ни второй способ нахождения суммы величин (с помощью прямоугольника) не помогают в нахождении суммы. Возникает противоречие: найти решение задачи нужно, но способ нахождения суммы дробей в этом случае неизвестен.
Дети возвращаются к способам нахождения суммы величин в первой и второй задачах.
Анализ задач и их решений показывает, что три задачи по смыслу одинаковые, следовательно, и решаются одним и тем же действием – сложением. Арифметическая операция одна и та же, но первоначально кажется, что результат сложения находится в каждом случае своим способом. При более глубоком анализе дети выясняют, что в первом и втором случаях сложение величин свелось к сложению натуральных чисел. Анализ решений второй и третьей задач показывает, что в обоих случаях значения величин записаны в виде дробей, которые нужно сложить. Но в одном случае решить задачу удалось, а во втором – нет. Почему? Во второй задаче нашли значение суммы: решение удалось свести к сложению натуральных чисел, так как у дробей одинаковые знаменатели (одинаковые мерки – восьмые доли), а во втором случае знаменатели разные.
Формулируется учебная цель: найти способ сложения дробей с разными знаменателями.
Дети возвращаются к известным им способам. Первый ‒ перевести длину пути в сантиметры и решать задачу в этих единицах измерения − решения не дает. Можно перевести длину в миллиметры и решить задачу. Но такой способ нельзя назвать общим, так как данное решение зависит от «хорошести» знаменателя.
Анализ второго способа показывает, что он дает возможность найти принцип сложения дробей с одинаковыми знаменателями. А в третьей задаче знаменатели (мерки) разные, поэтому дроби сразу сложить нельзя.
Дети приходят к выводу, что нужно конструировать еще один способ сложения дробей. Для этого они предлагают воспользоваться моделями дробей: на одном и том же прямоугольнике нужно заштриховать 3/8 этого прямоугольника и 5/12 этого же прямоугольника. Но в первом случае прямоугольник нужно разделить на 8 равных частей, а во втором – на 12 равных частей. Дети, обсуждая возникшую проблему в группах, находят выход: предлагают разделить прямоугольник на такое количество частей, которое будет делиться на 8 и делиться на 12. Это число 24. Нужно нарисовать прямоугольник и разделить его на 24 части, а потом изобразить на нем нужные нам дроби. Таким образом, дети самостоятельно приходят к идее поиска общего знаменателя и замене дробей 3/8 и 5/12 равными им дробями, но со знаменателем 24. А как только знаменатели стали одинаковыми, эти дроби можно изобразить в виде частей одного и того же прямоугольника, тогда сложение дробей сведется к сложению натуральных чисел.
В процессе поиска способа сложения дробей с разными знаменателями дети фиксируют свои рассуждения на рисунках дробей. В тетрадях получаются следующие записи:
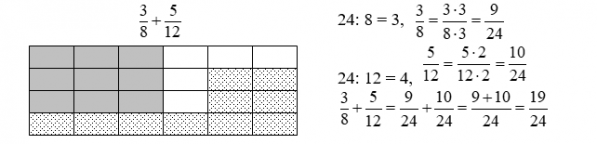
Вычисление суммы дробей с помощью прямоугольника ученики повторяют несколько раз: работая фронтально, работая в группе, работая в паре, самостоятельно. В результате они приходят к выводу, что так складывать дроби не очень удобно и очень долго. Появляется новая цель: сформулировать алгоритм сложения дробей. В результате анализа процесса сложения дробей с помощью прямоугольника ученики приходят к выводу: чтобы сложить дроби, нужно их привести к общему знаменателю (общей мерке) и сложить новые числители. Этот вывод дети фиксируют в виде блок-схемы.
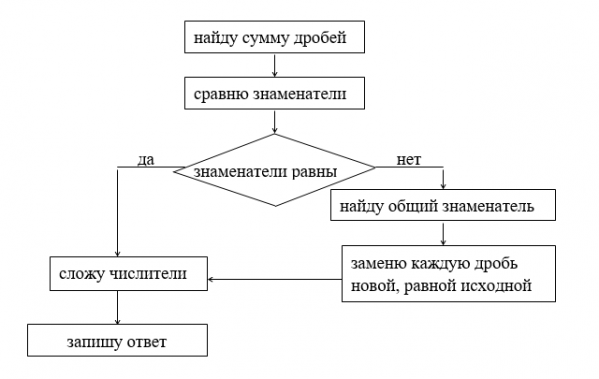
Затем этот общий принцип дети преобразуют в алгоритм сложения дробей, зафиксированный в виде памятки.
Работая с памяткой, блок-схемой, ученик проговаривает все действия вслух, а потом во внутренней речи. Благодаря тому, что при создании алгоритма сложения дробей с разными знаменателями школьники работают с предметными моделями дробей, рисуют их, преобразовывают, ученики присваивают способ действия. И что важно, в это время они не делают ошибок в вычислениях.
Для проверки нашего предположения, что использование предметных действий, построение моделей помогут ученикам научиться безошибочно находить суммы разного рода дробей, было проведено экспериментальное обучение. В эксперименте участвовали 52 пятиклассника. Безошибочно справились с вычислениями 88,4 %, остальные сделали по одной-две ошибки. Таким образом, подтвердилось наше предположение о том, что при обучении сложению дробей полезно использовать схему: вещь – действие – слово и образ – действие – вещь (предметное действие – образ – правило).
Опыт показывает, что при изучении числовых множеств данная схема практически работает всегда.
Итак, анализ литературы, наблюдения за учащимися на уроках показывают, что при изучении естественно-математических дисциплин возникает противоречие между абстрактностью усваиваемого содержания и проблематичностью его усвоить в силу несформированного абстрактного мышления. Преодолеть это противоречие можно, если при усвоении материала ученик получает информацию, оперируя предметами, образами, символами, комментируя свои действия. Тогда материальное действие трансформируется в идеальное знание и наоборот.
Более того, работа по схеме: вещь – действие – слово и образ – действие – вещь (предметное действие – образ – правило) будет способствовать формированию соответствующей учебному предмету способности.
Список литературы
- Апраушев, А. В. Рукотворение души / А. В. Апраушев. – Москва: Знание, 1986. – 96 с.
- Давыдов, В. В. Теория развивающего обучения / В. В. Давыдов. – Москва: ИНТОР, 2004 – 288 с.
- Клайн, М. Математика. Поиск истины / М. Клайн – Москва: Мир, 1988. – 295 с.
- Колмогоров, А. Н. Математика – наука и профессия / А. Н. Колмогоров. – Москва: Наука. 1988. − 288 с.
- Пиаже, Ж. Психология интеллекта / Ж. Пиаже. – Санкт-Петербург: Питер, 2004. – 192 с.
- Реньи, А. Трилогия о математике / А. Реньи – Москва: Мир, 1980. – 376 с.
- Сухотин, А. К. Философия математики: учебное пособие / А. К. Сухотин – Томск: Изд-во Том. ун-та, 2004. – 230 с.
- Фопель, К. Психологичеcкие принципы обучения взрослых. Проведение воркшопов: семинаров, мастер‑классов / К. Фопель. – Москва: Генезис, 2016 − 430 с.
- Холодная, М. А. Психология интеллекта: Парадоксы исследования / М. А. Холодная. – 2-е изд., перераб. и доп. – Санкт-Петербург: Питер, 2002 – 272 с.
- Эльконин, Б. Д. Введение в психологию развития (в традиции культурно-исторической теории Л. С. Выготского) / Б. Д. Эльконин. – Москва: Тривола, 1994. − 168 с.