Современные системы оценки знаний учащихся (ВПР, МЦКО, ЕГЭ, ОГЭ) основаны на выборе одного или нескольких ответов из предложенного списка. Задачи с развернутым ответом предполагают решение по заранее известному алгоритму. Такая система в течение продолжительного промежутка времени создает у ученика стереотип, что любая задача имеет единственное правильное решение. Но, если ученику предложить задачу, имеющую несколько решений, то это сразу же создает трудности как в решении, так и в осмыслении самой задачи. Развитие же творческого мышления – способности преодолевать и переосмысливать стереотипы – является необходимой задачей для обучения и воспитания действительных специалистов в своей области, способных решать задачи любой сложности. Для этого необходимо решать соответствующие задачи, которые имеют несколько разных решений со своими достоинствами и недостатками. В нашей работе они называются творческими задачами. Умение находить эти решения, а также видеть их недостатки в рамках предложенной задачи является необходимым для преодоления стереотипов, создаваемых тестами и шаблонами. Но каким образом оценивать, развивается ли творческое мышление ученика?
Оценка творческих способностей учащихся всегда была непростой задачей. Как правило, она формируется из большого числа критериев, в основе которых разные методы оценки. Кроме того, в каждом из этих методов необходимо участие внешнего наблюдателя, который и производит оценку по критериям. Получается, что наблюдатель фактически участвует в эксперименте наравне с испытуемым. Приведем пример на решении теста Торренса1 на оценку креативного мышления: например, фигура, нарисованная учащимся, не входит ни в одну таблицу оценивания, и в этом случае уже проверяющему придется решать, в какую из предложенных категорий ее относить. Взгляд внешнего наблюдателя субъективен, поэтому он поставит столько баллов за фигуру, сколько, на его собственный взгляд, ей стоит поставить, исходя из классифицируемой группы в таблицах. Безусловно, классические тесты предусматривают соотнесение ответов учеников между собой с целью учета повторяемости ответов, но это не дает полной объективной оценки.
Еще одним фактором, осложняющим оценку творческого мышления с помощью классических тестов, является ручная проверка работ. Сравнение ответов уже 15 учащихся значительно замедляет и без того непростой процесс проверки, а масштабирование тестов представляется маловозможным для одного учителя. Возникает потребность в таком способе оценки творческого мышления, который можно было бы цифровизировать и перевести в онлайн-режим с одновременной проверкой ответов без сравнения с таблицами в ручном режиме. Это максимально облегчит и упростит процесс оценивания, что сделает возможным решение творческих заданий прямо во время обычного урока. Создание же сайта или приложения для такой оценки полностью позволит освободить учителя от бумажной работы, а встроенные алгоритмы сразу будут выдавать статистические и персональные результаты по группам учеников за минимальное время автоматически.
В работе2 уже осуществлялась попытка создать цифровой критерий для оценки показателя творческого мышления путем присвоения баллов за ответы с помощью последовательности Фиббоначи и алгоритмизации подсчета ответов, однако учитывалось не само содержание ответа, а число заполненных форм для ответа, что, безусловно, являлось самым уязвимым местом такой системы. Учащиеся в определенный момент понимали, что учитывается число заполненных полей, а не суть ответа, поэтому начинали предлагать большое число одинаковых ответов по сути, искусственно повышая свой показатель творческого мышления. Для учителя такая ситуация приводила к тому, что работа снова сводилась к проверке в ручном режиме, так как отсеивать одинаковые ответы система не могла в связи с выбранным алгоритмом проверки.
Для подобной оценки необходимо выбрать такой параметр, который окажется независимым ни от ученика, ни от наблюдателя в эксперименте, на который может повлиять только испытуемый. Одновременно необходима возможность сравнивать решения между собой и численно их оценивать, иначе новый тест не будет отличаться от уже существующих. Сравнение чисел значительно проще, чем рисунков, и возможность оцифровывания такого критерия появляется по умолчанию.
В качестве такого критерия при оценке творческого развития учащихся выбрано число слов [1], которые ученик предлагает в решении творческого задания. Сравнительная оценка классических тестов творческого мышления и предлагаемого авторами подхода показала, что оценка получается даже более достоверная, чем получаемая в классических тестах [2]. Предложенный подход позволил сформировать набор критериев [3] для оценки творческого мышления школьников 8‒9-х классов с помощью новой цифровой системы Creo Datum [4; 5].
Принципиально новым является подход к выбору набора критериев [3], а именно анализ, сравнение и структура подсчета числа слов в ответах учащихся на поставленную задачу. Приведем краткое описание работы нового алгоритма, предложенного в новой архитектуре работы Creo Datum:
- Первоначальная обработка набора слов: все слова расставлялись по алфавиту, приводились к начальной форме (инфинитиву или именительному падежу и единственному числу), удалялись знаки препинания и цифры.
- Каждому слову присваивался 1 балл (пример: если в наборе 15 слов, то изначально ученик имел 15 баллов).
- Подсчитывалось число слов в двух категориях ответов: в предложенных идеях и критике этих идей, слова образовывали два набора.
- Удалялись незначимые части речи: союзы, предлоги, частицы, местоимения, числительные, незначимые глаголы, удалялись повторяющиеся слова.
- Далее ответы обрабатывались с помощью отдельно сформированной таблицы терминов и синонимов. В случае наличия слов-терминов в наборе ученика балл за каждое слово понижался на 20 %, а в случае наличия слов-синонимов, наоборот, каждый раз увеличивался (например, в случае наличия набора «алчный, жадный, корыстолюбивый» за первое слово ученик получал 1 балл, за второе ‒ 1,1, за третье – 1,2 и так далее). Чем более творческий подход ученик проявлял, тем больше баллов мог получить.
После предварительной обработки ответов происходило сравнение наборов ответов каждого ученика с общим набором ответов класса следующим образом:
- Для каждого слова считался коэффициент вхождения – сколько раз слово встретилось в общем наборе ответов.
- Балл за это слово делился на коэффициент вхождения (изначально каждое слово весит 1 балл; если оно встретилось у 4 участников, то 1 делится на 4, то есть ученик в итоге получает 0,25 балла).
- После пунктов 1‒7 суммировались измененные баллы по словарным наборам.
- Полученные числа для набора «Идеи» и «Критика» делились на исходные суммы наборов из пункта 4 (например, в идеях было 15 слов, стало 10,5, после деления получаем 0,7, аналогично для критики).
- Показатели дивергентности и конвергентности, получаемые исходно системой, умножались на соответствующие коэффициенты из пункта 9, затем суммировались полученные результаты, получая итоговый показатель творческого мышления.
Такой подход позволил максимально персонализировать ответы каждого участника, в данном подходе искусственно повлиять на рост показателя творческого мышления крайне трудно. Например, при увеличении числа одинаковых ответов, то есть увеличении числа одинаковых слов, их доля от общего числа значительно растет, но система их удаляет. Значит, доля уникальных слов значительно уменьшается, что приведет к общему падению значения творческого мышления.
Работа с цифровой системой и значение рассчитываемых параметров
Для получения корректных значимых результатов в любой системе необходимо понимать, какой принцип заложен в основе ее работы. В настоящий момент в основу работы цифровой системы Creo Datum заложена оценка словарных наборов испытуемых, сравнение и анализ которых происходит с формированием впоследствии необходимых параметров для оценки творческого развития учащихся.
Основные параметры и факторы, которые будут нами рассмотрены далее, следующие:
- ИКИ – итоговый коэффициент идей – коэффициент, отражающий уникальность словарного набора по идеям ученика, предложенным для решения творческого задания.
- ИКК – итоговый коэффициент критики – коэффициент, отражающий уникальность словарного набора по критике идей ученика, предложенных в качестве недостатков решений творческого задания.
- ТМ – творческое мышление – рассчитанное значение творческого мышления, в котором учтены такие факторы, как сложность каждого последующего решения и критического замечания, а также уникальность ответа в сравнении с группой испытуемых.
- Группа N – группа, к которой по результатам решения творческих задач система относит ученика, при этом хронология для каждого ученика видна учителю в его профиле.
- СЗ№ – среднее значение группы, в которую система определила ученика при выполнении задания. Показатель также рассчитывается на основе получаемых результатов каждой группы отдельно.
- ГТМ – график творческого мышления – наглядная визуализация значений творческого мышления, расположенных последовательно по временной шкале друг над другом для удобства сравнения; с ними одновременно показываются средние значения по группам учащихся пунктирной линией.
- Дополнительно: КИ и КК – коэффициент идей и коэффициент критики, – контрольные показатели, доступные только учителю: по ним возможно определить, списывает ли ученик у другого или нет.
ИКИ и ИКК отображают только рассчитанную долю уникальности ответа ученика в двух категориях – идеи и критика идей. Алгоритм учитывает число совпадений и повторяемость слов в ответе внутри всей группы. Одновременно с этим заложено [3] исключение разных категорий слов и учтены особые параметры ответа. Подробное описание работы с ИКИ и ИКК будет рассмотрено ниже.
Задания системы выдаются по усмотрению учителя и в соответствии с уровнем группы испытуемого, подробный механизм и анализ результатов будут приведены ниже. Сами задачи распределены на 3 уровня: 1-й уровень соответствует задачам, составленным по пройденному материалу по предмету. Пример: что может произойти с веществом при нагревании? Решения таких задач, как правило, лежат на поверхности и легко находятся большинством учащихся. Задачи 2-го уровня соответствуют задачам, материал по которым пройден, но уже содержат неочевидные решения. Пример: как может изменяться массовая доля вещества в растворе при пропускании в него SO3? И задачи 3-го уровня имеют в основе как известный материал, так и еще не изученный. Пример: предложите способы вернуть белизну пожелтевшей бумаге без потери информации на ней. Найти несколько решений уже является нетривиальной задачей, особенно в условиях недостаточности теоретических знаний. В формирование итогового значения творческого мышления для задач уровней 2 и 3 входят повышающие коэффициенты, которые дополнительно увеличивают значение творческого мышления после первичной обработки ответа ученика. Удивительно, но формировались повышающие коэффициенты не по решениям учеников, а по числу учеников, приступивших к решению задачи. Наблюдения показали, что значимая часть участников даже не приступают к более сложным задачам, так как не представляют, что можно предложить в качестве решения, если оно неочевидное и не лежит на поверхности.
В данной работе ученикам предлагались для решения задания на химическую или близкую тематику. Авторы считают, что будущим химикам развитие творческого мышления необходимо по многим причинам, в том числе ввиду сложности изучаемых процессов, установок и промышленных производств, где одновременно решаются сложные задачи, требующие комплексного подхода к решению. Достаточно привести простой пример: в раствор гидроксида кальция пропускают углекислый газ, при этом выпадает осадок массой 20 грамм. С одной стороны, решение очевидно: ученик пишет реакцию до карбоната кальция, считает объем поглощенного газа, получает ответ. Но, с другой стороны, можно найти и второе решение: гидроксид кальция реагирует полностью, выпадает осадок бóльшей массы, который затем растворяется, и остается 20 грамм осадка. И если первое решение находит подавляющее большинство учеников, то второе получают единицы. Развитие творческого мышления позволит ученикам обдумывать разные аспекты условия, чтобы находить все возможные решения.
Группы учащихся формировались системой автоматически по значению творческого мышления. Внутри системы проводится сравнение значения со средним по группе при выполнении конкретного задания, причем этот показатель переменный и зависит только от качества и количества ответов учеников этой группы. Группа 1 – группа, в которой значения творческого мышления не превышают 50 % от среднего значения; группа 2 – группа, значения творческого мышления учеников которой лежат в диапазоне от 50 % среднего значения до 150 % среднего значения (математически доказано, что среднее значение, умноженное на 1,5, не превосходит максимального значения выборки). И группа 3 – группа, в которой значения лежат от 150 % среднего значения до максимального, полученного данной группой.
Таким образом, система определяет группу, исходя из уровня ответов, классифицируя фактически по принципу: «продвинутая группа», «средняя» и «отстающая» (названия групп условные). Отметим, что такая градация в классификации установлена, исходя из того, что для значимого развития чего-либо необходимо преодолевать порог выполнения любого задания хотя бы на 50 %. Для второй группы полученные значения лежат от 50 % до 75–80 %, в зависимости от значений группы, что показывает достаточно хорошую работу. И значения от 80 % до максимума показывают, что ученик проявляет старание и рвение в выполнении задания. В зависимости от способностей учащихся реперные значения при разделении по группам можно установить в ручном режиме в настройках системы (например, группа 1 – от 70 до 80 %, группа 2 – от 80 до 90 %, группа 3 – от 90 до 100 %). Показатель является зависимым только от значений группы учеников, решающих задачи, то есть выступает объективным критерием оценки именно этой группы.
Стоит отметить, что работоспособность системы не зависит от числа человек внутри группы учащихся и выдает достоверные результаты, даже если задания выполняет всего один ученик, однако этот материал будет опубликован отдельно.
Методика оценки и анализа результатов решений творческих заданий
Рассмотрим методику оценки творческого мышления учащихся на примере группы детей одного класса школы имени В. В. Маяковского, участвующих в выполнении творческих задач в цифровой системе Creo Datum с 8-го по 9-й класс в 2023/24 и 2024/25 уч. гг. Опытная работа проходила с марта 2024 г. по апрель 2025 г. Группа состояла из 11 учеников. В качестве примера получаемой таблицы результатов приведем значения от апреля 2025 г. (табл. 1) для первой задачи.
Таблица 1
Пример результатов обработки ответов учащихся
на творческую задачу
Table 1
An example of the results of processing students' responses to a creative task
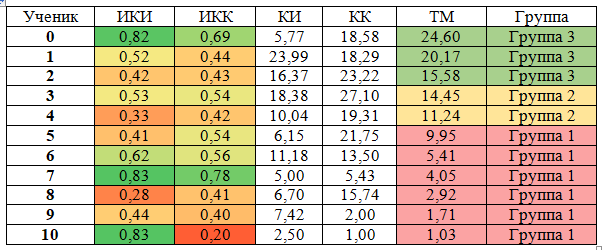
В течение опытной работы задачи для групп выдавались разные: первые 3 раза вся группа выполняла задачи первого уровня сложности, второго и третьего последовательно. После формирования устойчивого разделения по группам задачи распределялись следующим образом: группа 1, с наименьшими показателями ТМ, получала задачи уровней 1,1 и 2, то есть решали более простые задачи; группа 2 получала задачи уровней 1,2 и 3, то есть продолжала решать задачи с последовательным увеличение сложности; группа 3 получала задачи уровней 2,3 и 3, то есть более сложные для решения. Распределение задач таким образом позволяет повышать уровень ТМ, что будет описано и доказано ниже.
Продемонстрируем, что такие показатели, как группа ученика и коэффициенты ИКИ / ИКК, позволяют достоверно оценивать творческое развитие, а также анализировать самостоятельность выполнения заданий.
На рисунке 1 показаны распределения учащихся по группам в течение всей опытной работы. Для большинства учеников (1, 3, 4, 6, 9) наблюдаются закономерности в распределении по группам, например, ученик 3 с высокими показателями ТМ регулярно попадает по результатам решения задач в группу 3, аналогичная ситуация и у учеников 4 и 9. Для учеников 1 и 6 наблюдаются закономерности: ученик 1 качественно подходит к выполнению первых двух заданий, а на последнем уже не сосредотачивается полноценно, из-за чего происходит уменьшение показателя ТМ. Для ученика 6, напротив, заметен рост показателя ТМ в течение времени, что говорит о прогрессе в формировании и развитии творческого мышления.
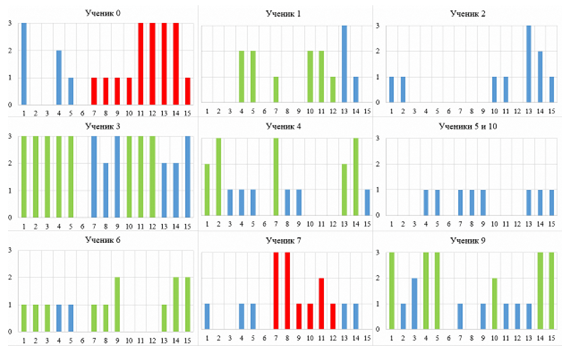
Рис. 1. Распределение учащихся на группы по решению задач
в процессе опытной работы: вертикальная ось – номер группы,
горизонтальная ось – порядковый номер решаемой задачи
Fig. 1. The distribution of students into groups for solving problems
in the process of experimental work: the vertical axis is the group number,
the horizontal axis is the ordinal number of the problem being solved
Для учеников 2, 5 и 10 заметны низкие результаты, это связано как с редким посещением уроков, так и с низкой успеваемостью в целом, что не позволяет говорить о каких-либо положительных тенденциях в развитии ТМ.
Ученики 0 и 7 наиболее интересны с точки зрения оценки ТМ, так как демонстрируют аномалии (красным цветом на рис. 1) в распределении по группам, то есть из 1-й группы попадают сразу в 3-ю группу, а затем снова оказываются в 1-й, что нехарактерно ни для одного другого ученика. Из оценки работы на уроке и текстовых ответов учащихся установлено, что они пользовались интернет-ресурсами при ответе на вопросы, но так как учителю необходимо быстро оценить, списывал ученик или нет, без проверки и сравнения текстовых ответов, то рассмотрим параметры разделения на группы и ИКИ / ИКК – коэффициенты более подробно.
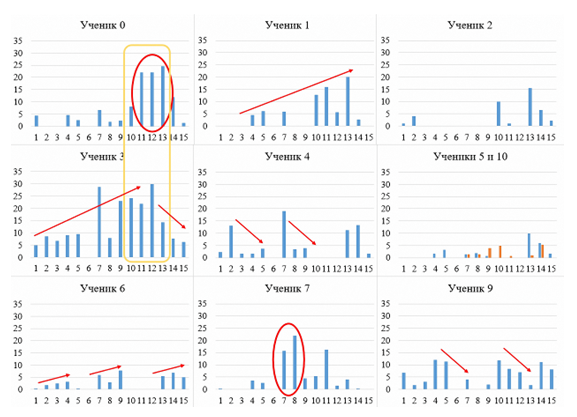
Рис. 2. Распределение и динамика баллов ТМ по ученикам:
вертикальная ось – балл,
горизонтальная ось – порядковый номер решаемой задачи
Fig. 2. Distribution and dynamics of TM scores by students:
the vertical axis is the score,
the horizontal axis is the ordinal number of the problem being solved
Первым характеристичным числом в оценке распределения по группам является балл, полученный учеником при выполнении заданий. Для учеников 1, 3, 4 и 6 наблюдается корреляция между тенденцией изменения баллов и распределением в группу по уровню, при этом для учеников 1, 3, 4 и 6 наблюдается рост творческого мышления за период проведения опытной работы. Падение балла у этой группы учеников в конце опытной работы связано с тем, что выдавались задачи повышенного уровня сложности, теоретический материал к которым еще не изучался (или изучался давно), однако тенденции на рост сохраняются. Напротив, у учеников, которые не заинтересованы в творческой деятельности (5, 10 и 9), получаемый балл остается неизменным или очень низким относительно всей группы учеников. Для ученика 2 видно, что даже редкое посещение уроков не препятствует творческому развитию – балл повышается, хотя и не так значимо, как у других учеников. Отдельного внимания заслуживают ученики, пользующиеся интернет-ресурсами при выполнении заданий. На графиках отмечены аномальные зоны резкого роста творческого мышления, сопровождающиеся затем резким падением. Происходит 4- или 5-кратное увеличение балла, не наблюдающееся ни у одного ученика, и без регулярного повторения, как, например, у учеников 4, 6 или 9. При этом сложность заданий увеличивается. Например, для ученика 3 видно сглаживание гистограммы относительно предыдущей попытки, тогда как у ученика 0 взрывной рост показателя творческого мышления (отмечено на рис. 2 желтым прямоугольником). Визуально по гистограмме достаточно сложно определить, является ли этот всплеск списыванием или внезапным появлением мыслей, поэтому покажем, как введенные коэффициенты ИКИ и ИКК позволяют делать выводы о качестве решения задач учениками.
Проследим и оценим динамику изменения показателей ИКИ и ИКК (рис. 3), которые видны учителю вместе с баллами ТМ и списком выданных заданий. Поскольку с повышением сложности заданий число ответов ученика должно уменьшаться, ИКИ и ИКК начинают сильнее зависеть от ответов других учеников, так как решения будут совпадать чаще, как и ключевые слова. Поэтому резкого роста при честном решении задач наблюдаться не должно. Однако тенденция роста к ключевым показателям уникальности (70 %) должна присутствовать, что мы и наблюдаем у учеников 1, 3 и 6 и по показателю дивергентности (ИКИ), и по показателю конвергентности (ИКК). Для других учащихся наблюдается рост одного из коэффициентов либо понижение из-за повышения сложности задач. При этом пересечение граничной отметки происходит случайным образом, например, у учеников 4 или 9. Однако для учащихся 0 и 7 на графиках заметно резкое увеличение коэффициентов ИКИ и ИКК с одновременным пересечением реперной прямой, хотя при этом линии тренда остаются ниже. Все эти факторы указывают на то, что рост ИКИ и ИКК создан искусственно, за ученика «выполняет» задание Интернет.
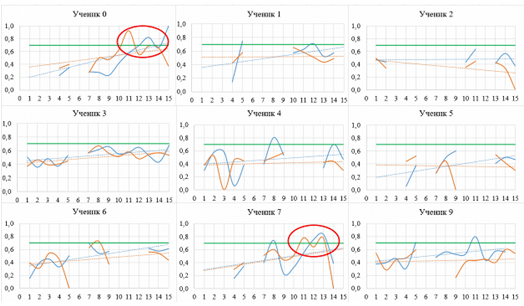
Рис. 3. Динамика изменения показателей ИКИ и ИКК:
синяя кривая – показатель ИКИ, оранжевая кривая – показатель ИКК;
вертикальная ось – доля уникальности ответа,
горизонтальная ось – порядковый номер решаемой задачи
Fig. 3. Dynamics of changes in indicators of ICI and ICС: the blue curve
is the ICI indicator, the orange curve is the ICC indicator; the vertical axis
is the percentage of uniqueness of the answer, the horizontal axis
is the ordinal number of the problem being solved
Дополнительным аргументом в пользу вышеприведенных рассуждений и эффективности предложенной методики является анализ еще нескольких расчетных величин: динамика роста балла по каждой задаче относительно первоначального (рис. 4) и стандартное отклонение от средних значений коэффициентов ИКИ и ИКК по каждой задаче (рис. 5). Рассматривая динамику роста балла, можно заметить, что для добросовестных учеников это монотонная зависимость, либо возрастающая, либо без существенных изменений (рис. 4). В случае же недобросовестного решения наблюдаются изломы роста, то есть график идет сначала на понижение, а затем резко растет, как у ученика 0, либо фрагментами, то быстрее, то медленнее, на коротком отрезке решений, как у ученика 7. Для ученика 3 тоже наблюдается излом, однако, как мы видим из показателей, рост на обоих отрезках постоянный и пропорциональный, то есть ученик стал лучше решать задачи, а не списывать готовые ответы.
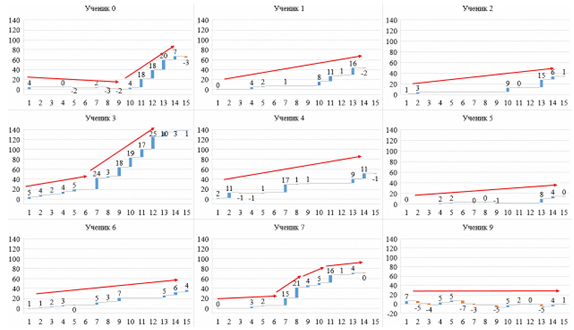
Рис. 4. Динамика роста балла относительно первоначального балла:
вертикальная ось – балл,
горизонтальная ось – порядковый номер решаемой задачи
Fig. 4. Dynamics of the growth of scores for tasks relative to the first solved task: the vertical axis is the score, the horizontal axis is the ordinal number
of the problem being solved
Стандартное отклонение от средних значений коэффициентов ИКИ и ИКК по каждой задаче позволяет также оценить достоверность получаемых данных: доверительный интервал, отмеченный на рисунке 5 синей и оранжевой линиями, то есть расхождения со средним значением, дает понять следующее: систематическое отклонение свидетельствует о том, что решения дает машина, а не человек.
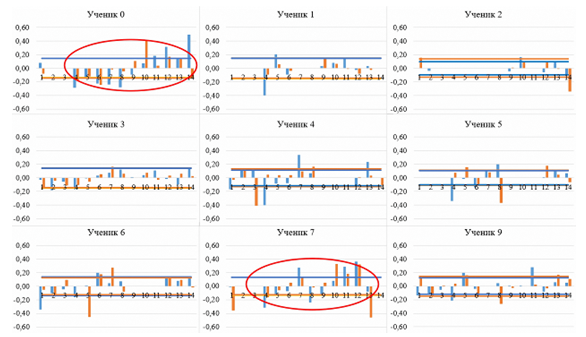
Рис. 5. Стандартное отклонение от средних значений
коэффициентов ИКИ и ИКК: оранжевые значения – доверительный интервал
и значения ИКК, синие значения – доверительный интервал и значения ИКИ; вертикальная ось – доля коэффициентов от среднего значения по задачам,
горизонтальная ось – порядковый номер решаемой задачи
Fig. 5. The standard deviation from the average values
of the coefficients ICI and ICC: the orange values are the confidence interval
and the IQ values, the blue values are the confidence interval and the IQ values;
the vertical axis is the proportion of coefficients from the average value of the tasks,
the horizontal axis is the ordinal number of the problem being solved
Для всех учеников группы, кроме 0 и 7, наблюдается случайное отклонение показателей ИКИ и ИКК от доверительного интервала, то есть происходит это в случайной задаче и для разных коэффициентов, соответственно. У учеников 0 и 7 коэффициенты ИКИ и ИКК целыми группами выходят за пределы доверительного интервала, что показывает нереалистичность этих результатов. Однако, если убрать заранее списанные результаты из набора данных, для учеников 0 и 7 графики приобретают общий вид, характерный для этой группы со случайно выпадающими значениями (рис. 6).
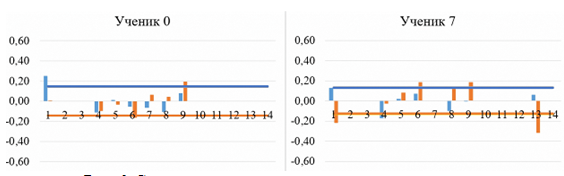
Рис. 6. Скорректированные стандартные отклонения
от средних значений коэффициентов ИКИ и ИКК:
оранжевые значения – доверительный интервал и значения ИКК,
синие значения – доверительный интервал и значения ИКИ;
вертикальная ось – доля коэффициентов от среднего значения по задачам,
горизонтальная ось – порядковый номер решаемой задачи
Fig. 6. Adjusted standard deviations from the average values
of the ICI and ICC coefficients: the orange values are the confidence interval
and the IСС values, the blue values are the confidence interval and the IСI values;
the vertical axis is the proportion of coefficients from the average value of the tasks,
the horizontal axis is the ordinal number of the problem being solved
Резервным критерием для отслеживания копирования и/или списывания ответов учеников друг у друга, а не из Интернета являются вспомогательные критерии КИ и КК, которые подсчитывают итоговое численное значение словарного набора ученика: если совпадают одновременно и значения ИКИ / ИКК и КИ / КК, следовательно, списывание происходит между учениками. В качестве примера приведем анализ одного из решений задачи (табл. 2).
Таблица 2
Результаты расчета показателей ИКИ / ИКК и КИ / КК
для списывающих учеников
Table 2
The results of calculating the indicators of ICI / ICC
and CI / CC is for cheating students

Полностью идентичные значения говорят о том, что и ответы учащихся идентичны друг другу. Для каждого ученика в группе в итоге формируется набор из пяти основных показателей, которые выводятся учителю на экран: ИКИ, ИКК, КИ, КК и ТМ. ИКИ позволяет делать вывод о том, насколько развита у ученика способность предлагать новые идеи к задаче и четко их формулировать. Чем выше ИКИ, тем больше решений предложил ученик и их проработал. ИКК позволяет оценить степень самокритичности, то есть способность находить недостатки в собственных решениях. Резкий рост на постоянной основе ИКИ и ИКК показывает, что используются интернет-ресурсы для ответов на задачи, то есть позволяет контролировать списывание из Интернета. КИ и КК помогают контролировать самостоятельность выполнения заданий внутри группы, то есть исключить списывание между учениками. И показатель ТМ позволяет судить о том, есть ли рост творческого мышления в целом. Наиболее показательно выглядит то (рис. 7), что соотношение ИКИ к ИКК для подавляющего большинства учеников смещено в пользу ИКИ, что обусловлено уже сформировавшейся привычкой у учеников к решению тестовых заданий формата ОГЭ и ЕГЭ, в которых всегда есть правильный ответ. Формулирование же критических замечаний в основном сложнее, занимает больше времени, поэтому идет выбор в пользу создания большого числа версий решения, но без поиска недостатков. Только небольшое число учащихся (например, ученики 3 и 7) стремятся соблюдать баланс между идеями и критикой, понимая, что обе составляющие важны в решении творческого задания.
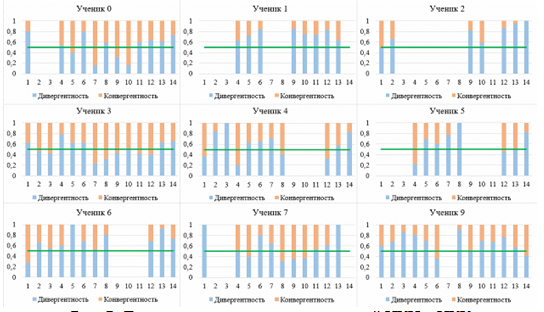
Рис. 7. Долевое соотношение показателей ИКИ и ИКК:
зеленая линия – граница соотношения 50 на 50 %
между коэффициентами; вертикальная ось – доля коэффициентов от 0 до 1,
горизонтальная ось – порядковый номер решаемой задачи
Fig. 7. The proportion of indicators of ICI and ICC:
the green line is the boundary of the 50-50 % ratio between the coefficients;
the vertical axis is the proportion of coefficients from 0 to 1, the horizontal axis
is the ordinal number of the problem being solved
Визуализация результатов для учителя и ученика
Общий результат решения творческих задач и для учителя, и для ученика отображается в виде графика творческого мышления (рис. 8, 9). На графике сплошными кривыми ‒ индивидуальные баллы ученика, пунктирными линиями отображены средние баллы по группе, к которой система отнесла этого ученика. Сравнивая положение обеих кривых на графике творческого мышления, возможно наблюдать закономерности его развития.
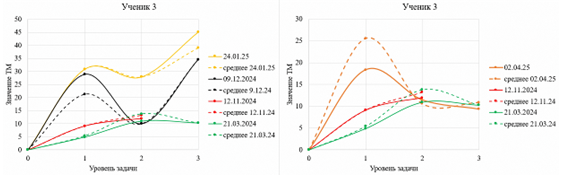
Рис. 8. Графики творческого мышления ученика 3
и средних значений по группе
Fig. 8. Graphs of student 3's creative thinking and group averages
На графиках ученика 3 мы видим, что этот ученик сам задает верхнюю планку своей группы, то есть фактически ее образует. Сплошные кривые идут выше или на одном уровне пунктирных, то есть ученик выше среднего уровня или является единственным участником уровневой группы. В таких случаях следует постепенно повышать сложность заданий, чтобы поднимать верхнюю границу сложности. Как видим, наблюдается планомерный рост показателя творческого мышления, а на черном графике заметно снижение балла, так как сложность задачи оказалась завышенной. Аналогичный график и по форме, и по значению соответствует решению от 2 апреля, когда выдавались группе самые сложные задачи. Балл творческого мышления ожидаемо снизился, однако остался на уровне с другими показателями в иные даты. Для 2-го и 3-го уровней задач ученик показал равные значения в группе, то есть снова стал лидером. Дальнейшее наблюдение продемонстрирует рост показателя творческого мышления в тех же рамках. Показатели ИКИ и ИКК при этом увеличиваются так же равномерно, что позволяет учителю видеть, что ученик развивается.
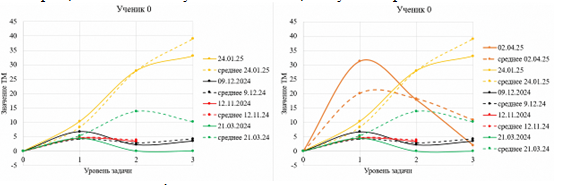
Рис. 9. Графики творческого мышления ученика 0
и средних значений по группе
Fig. 9. Graphs of student's creative thinking 0 and group averages
Анализируя график ученика 0, который, как было показано выше, списывает у других и пользуется интернет-ресурсами, сразу заметим большое различие в полученных баллах за январь и апрель, хотя до этого ученик вообще не показывал значимого развития и улучшения показателей. Сплошные кривые находятся значительно ниже пунктирных, что говорит о том, что ученик находится значительно ниже средних значений своей уровневой группы. За март, ноябрь и декабрь все значения примерно равны и не демонстрируют тенденций к росту, тогда как в январе и апреле идет рост в разы. Это доказывает, что ученик недобросовестно выполняет задания.
Созданный новый алгоритм обработки ответов учеников позволяет как качественно, так и количественно достоверно оценивать их творческое развитие. На начальном этапе работы с системой рекомендуется выполнить несколько подходов к решению задач, в примерах выше это решения от марта, ноября и декабря, чтобы заметить тенденцию развития у каждого школьника. На основании вышеприведенных данных можно реализовывать несколько стратегий развития учеников для каждой группы, укажем наиболее оптимальную, на наш взгляд, так как она полностью реализуется в созданной системе:
- Способные и мотивированные ученики (преимущественно группы 3 и 2) с каждым разом стараются лучше выполнить задание, им интересен сам процесс даже больше, чем итоговый результат. Для них следует подбирать задачи по мере усложнения, например, если изначально они шли по возрастанию сложности (1, 2, 3), то затем можно комбинировать либо (2, 2, 2 или 3, 3, 3), либо (2, 2, 3 или 2, 3, 3). Заметный рост графика творческого мышления будет означать, что задача уже перестала иметь какую-либо сложность в выполнении и следует перейти на ступень выше либо выбрать более сложную данного уровня. Понижение будет означать, что выбран достаточный уровень сложности и нужно продолжать, пока значения не начнут расти.
- Ученики группы 2 нуждаются в дополнительной проверке более сложным набором задач. Это необходимо для того, чтобы понять, случайно они попали в группу 2 или целенаправленно старались, чтобы повысить свой показатель ТМ. Таких учеников, согласно набранной статистике, порядка 10‒15 % от группы в целом, и при следующем решении задач почти всегда они переходят либо в группу 3, либо в группу 1.
- Ученики группы 1 самые сложные для анализа, так как среди них всегда есть те, у кого не получается решать подобные задачи в силу уже выработанной привычки к решению тестов, поэтому самому придумывать более сложные версии, кроме очевидных, очень сложно. Но по графикам творческого мышления их можно выделить, каждый раз их показатель будет расти, пусть и достаточно слабо. Такие ученики решают до конца все задачи из предложенных, несмотря на сложность. Те же ученики, которые бросают решать с первой же неудачной попытки, самостоятельно не способны развиваться только за счет решений творческих задач в системе, так как будут стараться списывать, пользоваться Интернетом и прочими источниками информации только потому, что часто за решение подобных заданий учитель стимулирует группу дополнительной оценкой по предмету.
Из таблицы 1 и по общей статике выполнения творческих задач в 8‒9-х классах видно, что из общего числа учащихся лишь порядка 20 % попадают в группу 3, еще около 10‒15 % оказываются в группе 2, то есть только 30 % от общего числа стараются выполнять задания качественно (не считая отдельных учеников группы 1, которые описаны выше, но таких единицы). Остальные 70 % в ряде случаев даже не пытаются приступить к выполнению заданий либо формально записывают одно тривиальное решение.
Учителю в цифровой системе для облегчения анализа и работы с большим количеством информации создается удобный интерфейс (рис. 10), куда выводятся графики творческого мышления по датам выполнения задач с возможностью выбора необходимого набора кривых, показатели ИКИ и ИКК, ТМ и группа ученика.
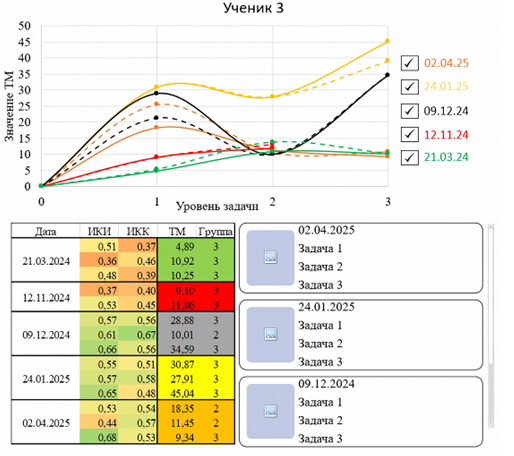
Рис. 10. Планируемый вид страницы ученика для учителя
в новой версии цифровой системы Creo Datum (в разработке)
Fig. 10. The planned view of the student's page for the teacher in the new version
of the digital Creo Datum system (under development)
На общей странице класса будет доступна общая таблица со средними значениями ТМ по группам и показателями КИ и КК для выявления недобросовестного выполнения задания. Возможность наблюдения и анализа как группы в целом, так и каждого ученика по отдельности позволит минимизировать время на проверку творческих заданий и максимально сосредоточиться именно на развитии творческого мышления учеников.
Список литературы
- Коваленко И. В., Оржековский П. А. Влияние используемого словарного набора при решении творческих задач по химии на оценку креативного мышления школьника // Учебный эксперимент в образовании. 2024. № 2 (110). С. 77‒86
- Коваленко И. В., Оржековский П. А. Сравнительный анализ классических тестов творческого мышления и цифровой среды Creo Datum по оценке творческого мышления школьников // Журнал педагогических исследований. 2025. № 3 (в печати).
- Коваленко И. В., Оржековский П. А. Повышение достоверности оценки показателя творческого мышления учеников в цифровой системе Creo Datum // Наука и школа. 2025. № 5 (в печати).
- Оржековский П. А., Степанов С. Ю., Мишина И. Б. О непрерывности оценки развития у обучающихся репродуктивных и креативных мыслительных действий // Непрерывное образование: XXI век. 2019. № 3 (27). С. 28‒39.
- Цифровая система Creo Datum : официальный сайт. Москва, 2020. URL:.https://www.creo-datum.ru/pages/sing_in.php (дата обращения 11.04.2025).